Cluster Mempool RBF Thoughts

[sdaftuar]

I think that if we don’t re-linearize what is left of the old clusters, that we might open the door to some RBF pinning scenarios that otherwise wouldn’t exist.

Imagine you are doing an RBF where you are swapping out one low fee parent with another. Old tx graph (feerates in parens, all txs same size):

graph TD
   P1("P1(1)") --> A("A (19)")
   P2("P2(9)") --> X("X(1)")
   P1 --> X
   P3("P3(1)")

This 2-cluster tx graph would have mempool chunks with feerates [10, 9, 1, 1].

And then you want to consider replacing A with B:

graph TD
   P1("P1(1)")
   P2("P2(9)") --> X("X(1)")
   P1 --> X
   P3("P3(1)")--> B("B(?)")

Assuming B’s feerate is going up, then if we didn’t relinearize the cluster containing A, the mempool chunks we’d get from this graph would have feerates: [(R(B)+1)/2, 5, 1]. If you were to relinearize, you’d instead get [(R(B)+1)/2, 9, 1, 1].

Using the feerate diagram test as our RBF metric, if we don’t relinearize, then I think you could just increase the size of P2 (and leave it at the same feerate) in order to increase the feerate required for B to be accepted. Not sure exactly what the mathematical relationship is, but this strikes me as a bad outcome?

Update:

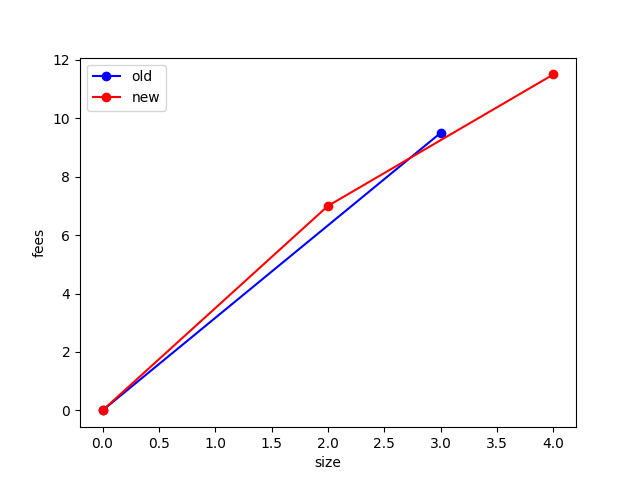
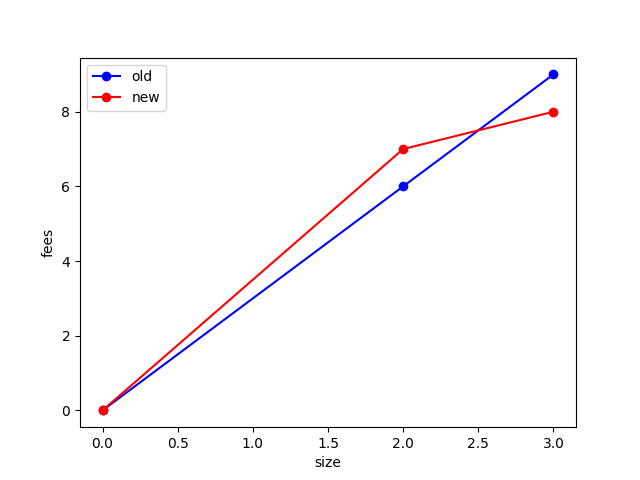
I did a quick check to see how high I could get the required feerate of B based on the (a) size of P2 (holding feerate constant), and (b) the feerate of P2 (in the range of 1-9), assuming we do/do not relinearize the old cluster when processing an RBF.

Changing P2’s size, fixing P2 at feerate 9:

P2’s size	Min fee bump with relinearization	Min fee bump without relinearization
1	1	4
2	1	6
3	1	6
4	1	7
8	1	8
9 & higher	1	8

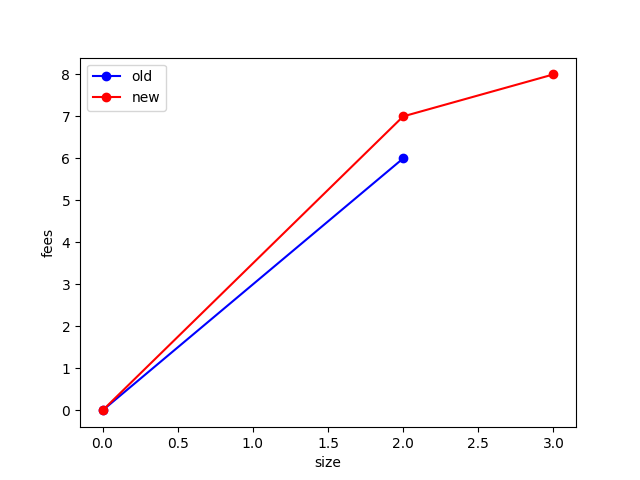
Changing P2’s feerate, fixing P2 at size 1:

P2’s feerate	Min fee bump with relinearization	Min fee bump without relinearization
1	1	1
4	1	2
6	1	3
8	1	4

My conclusion from this is that we ought to relinearize the old clusters, to avoid artificially increasing the fee bump needed due to unrelated transactions like P2 (and X, which is the only reason that P2 is relevant in the graph).

[instagibbs]

@sdaftuar

In this example, I don’t see how any of these proposed limits (2a, 2b, or 2c) would pose a path-dependence where seeing more RBFs makes C6 easier to get in.

I think 2a makes most sense, and is what I was leaning towards in Proposal for a new mempool design · Issue #27677 · bitcoin/bitcoin · GitHub

I always thought it likely fine if we had to drop that number from 100.

[sdaftuar]

(Not sure where else to put this, but wanted to log this somewhere)

I was thinking about Cluster size 2 package rbf by instagibbs · Pull Request #28984 · bitcoin/bitcoin · GitHub, and realized just now that the RBF rules there for the cluster-size-2 case has the same sort of problem that I brought up here, with regard to the RBF heuristic not quite lining up with the feerate diagram test that we’d like to use in the future.

Issue 1: The feerate diagram might not improve using the rules described in #28984.

This is similar to the example posted above. Imagine the starting mempool is:

graph TD;
    A[Tx A: sz 2, fee 4.5]-->B[Tx B: sz 1, fee 5];

And we want to process a package (C, D) that would make the mempool look like this:

graph TD;
    A[Tx A: sz 2, fee 4.5]
    C[Tx C: 1]-->D[Tx D: 6];

Imagine specifically that D conflicts with B.

Using the heuristic in the PR, we’d say the package feerate of (C, D) is 3.5, which is greater than the ancestor feerate of B (9.5/3), and the total fee of (C, D) is 7, which is more than 5.

However the feerate diagram does not strictly improve:

Issue 2: The rules proposed in #28984 might be satisfied when validating a package (A, B), but might fail to successfully relay if A is valid in a peer’s mempool and then B is evaluated using legacy RBF rules (as a singleton RBF).

Consider the same situation as above, but with feerates such that the package would pass validation rules (this could be accomplished by raising the fee for tx D sufficiently high).

Now suppose that tx C would relay to our peers, because it has a high enough feerate that it passes the mempool min fee and minrelayfee. Then using submitpackage (or package relay) to get (C, D) to our own node might still result in tx D failing to propagate, because once tx C propagates, then attempts to relay D will trigger the old RBF rules, which (in particular) prohibit an RBF that introduces a new unconfirmed parent.

So it would seem that to make package RBF of (C, D) useful, users would need to ensure that C would not relay on its own (eg by making its feerate below the minrelayfee).

Issue 3: In the new cluster mempool world, the feerate diagram might be satisfied for a transaction package (A, B), but fail to relay successfully if A is valid in a peer’s mempool and then B’s RBF attempt is validated using feerate diagram rules (which can fail because the starting diagram for a peer might include tx A).

It turns out that the feerate diagram test might not be strictly improved if we are able to break up a transaction package into its parts.

Consider this starting mempool, all transactions are the same size:

graph TD;
    A[Tx A: fee 1]-->B[Tx B: fee 5]

And we are considering a new package (C, D) where D conflicts with B, which would bring the mempool to this:

graph TD;
    A[Tx A: fee 1]
    C[Tx C: fee 3]-->D[Tx D: fee 4]

This would pass the feerate diagram check if (C, D) is evaluated as a package against the starting mempool:

However, if tx C were to relay on its own (it has no conflicts, so this is plausible), then the feerate diagram check for tx D versus a starting mempool of (A, B, C) would fail:

[EDIT: just realized the total fee didn’t go up, which is perhaps not a great example.]

[instagibbs]

Noting up front that these scenarios are what I’m calling “cross-sponsor” RBF, where the funding tx is sponsoring on package, then switches over to sponsor another parent. Typical example for a wallet would be they’re CPFPing something with a nice sized utxo, then another package becomes higher priority and they want to switch.

@sdaftuar

Issue 1: The feerate diagram might not improve using the rules described in #28984.

I don’t think it should be shocking miner scores isn’t strictly improving the mempool. I’m also unconvinced it’s worth stalling out limited package rbf given the current state of the art, which is substantially worse.

At the risk of re-adding a pin, changing the heuristic to:

1. for all direct conflicts, package feerate must exceed direct conflict’s feerate
2. for all conflicts(direct or indirect), package feerate must exceed ancestor feerate of conflict

may be something to double-check.

This is what https://github.com/bitcoin/bitcoin/pull/25038 had essentially implemented, which means the specific cross-sponsor RBF becomes relatively impractical.

Example test case for this using this “old” heuristic:

policy: Ephemeral anchors

@sdaftuar

Imagine specifically that D conflicts with B.

Or C with B, I believe that’s equivalent in this case.

@sdaftuar

Issue 2: The rules proposed in #28984 might be satisfied when validating a package (A, B), but might fail to successfully relay if A is valid in a peer’s mempool and then B is evaluated using legacy RBF rules (as a singleton RBF).

Gloria and I had this exact discussion prior: policy: nVersion=3 and Package RBF by glozow · Pull Request #25038 · bitcoin/bitcoin · GitHub

Wallet authors can avoid this in a fairly simple manner, by not “cross-sponsoring”. If they do, make it a 0-fee parent package via v3/ephemeral anchors, but note that if a counter-party has already sponsored the package, cross-sponsoring will still be disallowed since parent will still be in the mempool. Post-cluster mempool this issue goes away (except the mild pinning as you note in issue 3?)

Don’t have anything intelligible to say about issue 3 yet other than it’s interesting!

[instagibbs]

@sdaftuar

Issue 3: In the new cluster mempool world, the feerate diagram might be satisfied for a transaction package (A, B), but fail to relay successfully if A is valid in a peer’s mempool and then B’s RBF attempt is validated using feerate diagram rules (which can fail because the starting diagram for a peer might include tx A).

Seems like per-chunk processing allows for a mild “parent pays for child RBF”. The “cost” of doing per-chunk evaluation: people may be making cpfp chains one by one, and this will not be in lock-step with a whole package being gossiped at once. #26711-like solutions mean you get less of this asymmetry, at increased cost of complexity, and not always dealing with chunks.