Disclosure
Since there seem to be a few eyes on this now I thought I’d better disclose the issue I had hoped to silently patch before anyone really read this over. Over the weekend I’ve spent some time on implementing this scheme and found several problems with my writeup (to be addressed). More importantly, I discovered that when penalties are used, a malicious party can withhold their state update signature but collect everyone else’s so that they are the only one who can publish S+1, and honest parties are prevented from publishing state S because of the penalty. Thank you to everyone for the thoughtful feedback and further reading, I hope that I can plug this hole in the protocol and reply properly later this week. It’s possible this proposal may not survive the fix at all, unfortunately… I probably published this prematurely.
Introduction
Eltoo schemes have desirable properties such as simplicity, constant storage requirements, and compatibility with multi-party channels. However, naive eltoo is vulnerable to an attack where a dishonest party submits old update transactions in an attempt to delay settlement of the channel state until HTLCs have expired.
This proposes a multi-party eltoo scheme that both allows penalizing dishonest behavior, and provides a bounded settlement time. By giving parties only one chance to update the channel state on-chain, this scheme drastically reduces the ability of malicious parties to prevent honest settlement of the channel.
This proposal depends on a way to make signed vector commitments, and check vector committed items against a spending transaction.
I call this construct "multi-transaction-signature"s.
This proposal also depends on “floating transactions” (as used in other eltoo schemes).
Therefore, we will assume the LNHANCE soft fork, consisting of OP_INTERNALKEY (IK), OP_CHECKTEMPLATEVERIFY (CTV), OP_CHECKSIGFROMSTACK (CSFS), and OP_PAIRCOMMIT (PC).
In LNHANCE CTV+CSFS enables the “floating transactions” construct, and CTV+CSFS+PC enable this “multi-transaction-signature” construct.
I believe this scheme could be adapted to ANYPREVOUT(APO)+CSFS+PC however I’m admittedly less familiar with APO than I ought to be.
Prior Art
This is likely completely non-novel, but unfortunately I’m unfamiliar with most of the literature. My apologies to anyone whose work I almost certainly overlooked.
Acknowledgements
- Moonsettler for review, tentative approval, and driving the current LNHANCE efforts and propsing an opcode (
OP_PAIRCOMMIT) that enables this without all of the aspects of CAT that scare me. - ReardenCode for review, comments, and being open to discussion on xitter which encouraged me greatly in getting back into Bitcoin dev.
- Everyone else who read this mess of a draft and offered comments or encouragement (or not-so-encouragement, you know who you are! lol)
- The all of the Bitcoin giants out there, I’m not standing on your shoulders but I’m probably stepping on your feet.
Description
This scheme bounds the number of times an update transaction can be submitted for a multi-party channel by limiting each party to submitting a single update.
State updates occur similar to Decker, Russell, and Osuntokun eltoo by using CHECKLOCKTIMEVERIFY(CLTV) and an incrementing absolute timelock to ensure that update transactions can only be spent by either the appropriate settlement transaction or a newer update transaction.
To remove parties’ ability to update more than once, every state update consists of a large set of update transactions arranged into generations.
Every generation allows a party to submit an update, but removes that party from the set of parties eligible to submit an update in the future.
Each unique update transaction has a unique set of parties that are still eligible to submit updates.
Each generation 1 <= K < N has one transaction for every possible subset of length N - K of parties still eligible to submit updates.
These update transactions are divided into generations 1 < K < N of N choose K transactions each.
Generation 1 prohibits 1 party from updating any further and has N choose 1 transactions in it.
Generation 2 prohibits 2 parties from updating any further and has N choose 2 transactions in it.
Generation N-1 prohibits all but 1 party from updating.
The total number of all of these update transactions is ~2^N - 1 + N which obviously grows very quickly.
After an update transaction is accepted either because the last party submitted their update transaction, or by a timelock expiring, a settlement transaction splitting up the channel balance can be submitted as in other eltoo schemes.
This settlement transaction can optionally penalize misbehaving parties by dividing their channel balance among the honest parties.
This scheme as described so far, achieves both of the stated goals, bounding settlement time and optionally enabling punishment.
It does, however, require sharing 2^N signatures per party.
Using OP_PAIRCOMMIT we can instead sign a commitment which authorizes many transactions, requiring only a merkle proof proving that a given CTV template has been signed, which indicates a valid state transition.
This compression from 2^N signatures to one per party enormously reduces network communications required, and also makes it feasible to use musig to produce a single signature instead.
However, for the sake of reduced interactivity, this proposal will use one signature per party.
Outputs on each update transaction are Segwit v1, and have P=N-K tap leaves, one for every party still eligible to update.
The witness includes a merkle proof that the transaction has been signed for, as well as signatures on that merkle root from all parties (even ones no longer eligible to update), except for the updating party.
The updating party provides a regular SIGHASH_ALL signature which is checked with CHECKSIGVERIFY.
This ensures other parties cannot submit an update transaction on behalf of a different party.
Each tapscript follows a fixed path in the merkle tree, which binds it to transition to a specific transaction.
If parties could submit an arbitrary inclusion proof in their transaction, they could for instance fraudulently submit one that removes a different party from the eligible-to-update set.
To illustrate, here is what a generation 0 tap script (from the commitment TX) might look like for A to update.
Because party A is updating, the spending transaction must match the CTV template TX_BCD_TEMPLATE whose output is identical to this transaction, but without a tap leaf for A to submit another update.
This removes party A’s ability to update further.
In addition to this one, generation 0 would have equivalent tap leaves with scripts corresponding to each of the other parties in the channel.
witness: <DSIG> <CSIG> <BSIG> <GEN2_MERKLE_ROOT> <ABD_ABC> <TX_ACD_TEMPLATE> <TX_BCD_TEMPLATE> <sig(A)>
tapscript:
<S+1> CHECKLOCKTIMEVERIFY DROP # <DSIG> <CSIG> <BSIG> <GEN2_MERKLE_ROOT> <ABD_ABC> <TX_ACD_TEMPLATE> <TX_BCD_TEMPLATE> <sig(A)>
<A> # <DSIG> <CSIG> <BSIG> <GEN2_MERKLE_ROOT> <ABD_ABC> <TX_ACD_TEMPLATE> <TX_BCD_TEMPLATE> <sig(A)> <A>
CHECKSIGVERIFY # <DSIG> <CSIG> <BSIG> <GEN2_MERKLE_ROOT> <ABD_ABC> <TX_ACD_TEMPLATE> <TX_BCD_TEMPLATE>
CHECKTEMPLATEVERIFY # <DSIG> <CSIG> <BSIG> <GEN2_MERKLE_ROOT> <ABD_ABC> <TX_ACD_TEMPLATE> <TX_BCD_TEMPLATE>
SWAP # <DSIG> <CSIG> <BSIG> <GEN2_MERKLE_ROOT> <ABD_ABC> <TX_BCD_TEMPLATE> <TX_ACD_TEMPLATE>
PAIRCOMMIT # <DSIG> <CSIG> <BSIG> <GEN2_MERKLE_ROOT> <ABD_ABC> <BCD_ACD>
SWAP # <DSIG> <CSIG> <BSIG> <GEN2_MERKLE_ROOT> <BCD_ACD> <ABD_ABC>
PAIRCOMMIT # <DSIG> <CSIG> <BSIG> <GEN2_MERKLE_ROOT> <GEN1_ROOT>
SWAP # <DSIG> <CSIG> <BSIG> <GEN1_ROOT> <GEN2_MERKLE_ROOT>
PAIRCOMMIT # <DSIG> <CSIG> <BSIG> <GEN1_MERKLE_ROOT>
TUCK # <DSIG> <CSIG> <GEN1_MERKLE_ROOT> <BSIG> <GEN1_MERKLE_ROOT>
<B> # <DSIG> <CSIG> <GEN1_MERKLE_ROOT> <BSIG> <GEN1_MERKLE_ROOT> <B>
CHECKSIGFROMSTACK # <DSIG> <CSIG> <GEN1_MERKLE_ROOT> <1|0>
VERIFY # <DSIG> <CSIG> <GEN1_MERKLE_ROOT>
TUCK # <DSIG> <GEN1_MERKLE_ROOT> <CSIG> <GEN1_MERKLE_ROOT>
<C> # <DSIG> <GEN1_MERKLE_ROOT> <CSIG> <GEN1_MERKLE_ROOT> <C>
CHECKSIGFROMSTACK # <DSIG> <GEN1_MERKLE_ROOT> <1|0>
VERIFY # <DSIG> <GEN1_MERKLE_ROOT>
<D> # <DSIG> <GEN1_MERKLE_ROOT> <D>
CHECKSIGFROMSTACK # <1|0>
The templates are arranged into a proof tree structured like this:
GEN1_MERKLE_ROOT
GEN1_ROOT GEN2_MERKLE_ROOT
BCD_ACD ABD_ABC GEN2_ROOT GEN3_MERKLE_ROOT
TX_BCD_TEMPLATE TX_ACD_TEMPLATE TX_ABD_TEMPLATE TX_ABC_TEMPLATE |
|
/---------------------------------------------------------\
AB_AC_AD_BC BD_CD_DUMMY
AB_AC AD_BC BD_CD DUMMY
TX_AB_TEMPLATE TX_AC_TEMPLATE TX_AD_TEMPLATE TX_BC_TEMPLATE TX_BD_TEMPLATE TX_CD_TEMPLATE
Every party signs the merkle root GEN1_MERKLE_ROOT, and that set of N signatures is sufficient for a state update.
The presence of SWAP or NOP opcodes commits to the path in the merkle tree, and prevents invalid state transitions.
Party B’s script would instead have the sequence NOP PAIRCOMMIT SWAP PAIRCOMMIT SWAP PAIRCOMMIT since the TX_ACD_TEMPLATE which excludes B from further updates, is at index 1.
Party C’s script would have the sequence SWAP PAIRCOMMIT NOP PAIRCOMMIT SWAP PAIRCOMMIT since it is at index 2.
You can see how the index of the desired template in the ordered list of transaction templates corresponds to the SWAP and NOP opcodes as a little-endian representation of bits, with SWAP representing a 0 and a NOP representing a 1.
Later generations are encoded in the lower branches of the tree.
NOPs could be eliminated making some scripts shorter than others.
I think this would have pretty negligible effects on incentives, but it’s also simpler for me to think about with them in.
Without PAIRCOMMIT
This scheme works without PAIRCOMMIT but requires every party to share a signature for every valid state transition.
~2^N signatures, per party, need to be shared to make this scheme work without PAIRCOMMIT.
Transitions must be individually authorized, otherwise a blanket signature authorizing a transition to state S would permit any update transaction in R<S to transition into any update transaction in state S.
Consider a case where parties A,B, and C are eligible to update.
With blanket signatures from B, and C to state S, A could sign a transaction that transitions to a state where A and B are able to update, thereby stealing C’s update opportunity and preserving their own.
This is why each valid state transition must be authorized individually.
Practicality
Each party is required to recompute the entire multi-transaction-signature commitment every channel state update, and this involves computing ~2^N transactions and building a merkle tree committing to all of them.
This means that there are ~(N - 1) * 2^(N + 1) - 1 SHA256 operations required for a penalty scheme. (Take this math with a grain of salt, I haven’t proved it out)
A non-penalty scheme is around twice as fast because there is only one settlement transaction for all updates in a state, rather than one settlement transaction for every update in a state, this takes the complexity to ~(N - 1) * 2^N - 1.
For a penalty scheme this results in ~18431 SHA256 `operations for N=10 parties.
The amount of memory required should be logarithmic or better over N so memory should not be a limiting factor.
With a very plausible single core performance of ~1MHash/s on my aging mid-range desktop computer, that means calculating the commitment merkle root will optimistically take ~18ms.
State recomputation can be significantly parallelized, so with 12 threads that’s a best case scenario of 1.5ms.
This is all very optimistic and assumes the other computations in state recalculation take negligible time.
The practical limit for this scheme is probably in the 10-20 party range because the exponential growth more than doubles for every party added.
Using these very optimistic assumptions, 17 parties, a penalty scheme would take ~743ms to recalculate.
I unfortunately don’t know how many parties other schemes consider practical, but this scheme is fairly limited due to the exponential size of the number of potential update transactions that need to be computed.
Conclusion
I present a multi-party eltoo scheme with desirable functional properties but exponential computational complexity using one known technique and one likely known technique. What I’m calling a “multi-transaction-signature” permits a single signature to commit to multiple possible transactions representing state transitions. I suspect it’s a trivial variant of vector commitments too uninteresting to have a name. This scheme combines these "multi-transaction-signature"s with existing eltoo “floating transactions” to enable a communication-efficient multiparty eltoo channel with or without penalty, and with bounded settlement time. Parties are given one chance to update the on-chain state, and may (optionally) be penalized for publishing old state, which should make attacks economically unattractive. The amount of computation required of parties is exponential on the number of parties N, however I believe that N~=10 is practical in this scheme, and also nearing the practical limit of multi-party channels anyway, due to the liveness requirements of participants, and network latency. I present this scheme mostly to solicit feedback, is this interesting enough to deserve a better writeup? this is obviously very incompletel. Is it interesting enough to warrant an implementation? Maybe it is only rehashing previous work, if please direct me to it so I can familiarize myself. Maybe, (my hope) is it inspires one of you wizards to invent a better or related scheme.
Further Work
- Can this be safely integrated with a watchtower?
- Truncating the number of generations at some number
M < Ncould potentially drastically reduce the number of transactions to calculate and hash, as long as there are less malicious users than M it should remain secure. - Can this scheme be adapted to tolerate offline users? Each generation of update transaction already partitions the parties into two sets, it might be possible to use something like this to split and merge a multi party pool if parties also sign for a set of merge transactions? Maybe?. It’s worth exploring but there’s a lot of pitfalls, there might not be a (good) way to do it.
- Since state update communications are reduced to a single signature per party, is it practical to use musig instead, to reduce the witness size of uncooperative closes? That would require two rounds of communication, however it could still be practical.
- Is this interesting enough to implement? Maybe just to benchmark state update performance to gauge practical limits.
Copied from here: Multiparty Eltoo with bounded settlement and optional penalties · GitHub
I’ve started on a proof of concept implementation here, it is really rough and I’m only sharing it so other people can get benchmark numbers on their machines, there’s probably many bugs: GitHub - Ademan/multi-party-eltoo-with-bounded-settlement
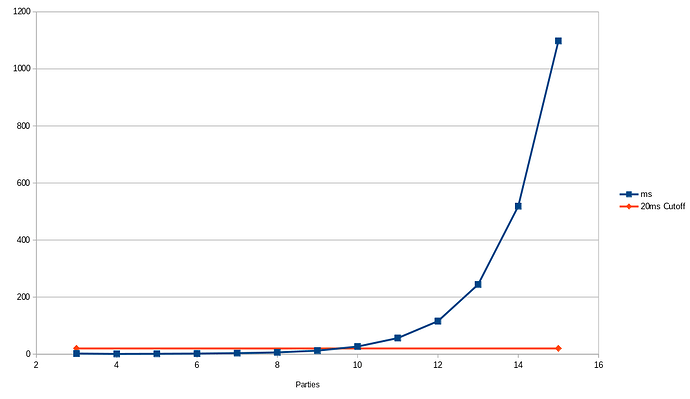
As could be expected from an exponentially growing complexity, this protocol maxes out fairly quickly, I’m using a 20ms cutoff per an anonymous suggestion, however I think 10-12 parties should be pretty possible on similar hardware. Everything about the current version is very naive and could be improved, probably not enough to hit 16 parties though.
On my 16 thread Ryzen 7 5700U (mobile processor) here’s a graph of time taken to recalculate state vs number of parties. It is already using multiple cores via rayon, but only in one place and in a very naive way.
Aside from general comments I’d like to know how many parties we’re really shooting for in a multi-party channel. Is this a dead end, or somewhat interesting?