Channel depletion, LN Topology, Cycles and rational behavior of nodes

[renepickhardt]

@ajtowns

For a given initial network state, is the resulting spanning tree reproducible/predictable?

I am not sure I understand your question correctly. My post said we can for a fixed wealth distribution predict the location of the spanning tree by solving the integer linear program. So I guess the answer is: Yes, if we knew the wealth distribution of coins on the network.

@ajtowns

Are there circumstances where the spanning tree change after being established, solely due to payments being made, without opening/closing channels (or changing fee rates)?

That I am not too sure about and I also listed it as an open question in my OP. Thus the following is mainly a summary of observations and conjectures:

Of course the initial wealth distribution has an impact to which channels deplete. For example, if I send away all my funds, then consequently all my channels will be depleted. But as that is an extreme state I would guess with fixed topology / fees the location of the spanning tree should be somewhat stable if arbitrary wealth distributions are being picked to test for this.

Actually I tried to adopt my code to track the location of the spanning tree while the wealth distribution changes (e.g. payments are being conducted). So far my impression is that the location is less stable than I would expect. E.g. Channels which are often not depleted are still depleted in about 50% of all tested wealth distributions. (Other channels are depleted much more frequently)

Somehow this makes sense as in my original simulation the network was never in the optimal fee potential state but only close to it and a payment changed the wealth distribution.

My problem: I haven’t found a good statistical measure / visualization for that yet. I will need more time to come back to that question.

@ajtowns

This seems to me like a bit like you’ve designed a network with an implicit “most expensive” spanning tree, and that the simulation simply exhausts all the cheaper paths until that’s what’s left?

No, I don´t think that is an accurate summary / description of what I tried to present.

Just to be clear I haven’t designed a network. I just tried to find a way to explain the emergent phenomena of channel depletion that most people observe and report about.

Once I understood that the existence of different cost cycles are the reason I found it quite simple to explain:

1. Imagine the network topology was actually a spanning tree to begin with. If Alice wants to pay x sats to Bob and then Bob wants to return those x sats to Alice the network would be back in the initial state (as every wealth distribution corresponds to exactly one liquidity state in a spanning tree)
2. Now, if on the other hand the network had cycles and the fees on the edges vary it is very likely that the flow of x sats from Alice to Bob goes along a different route than the return payment. (E.g. in the example below Bob would pay Alice via Carol)
3. Thus, the payment back and forth would actually flows along a cycle and contribute to deplete that cycle.
4. In particular depletion takes place even if we don’t have source and sink nodes.

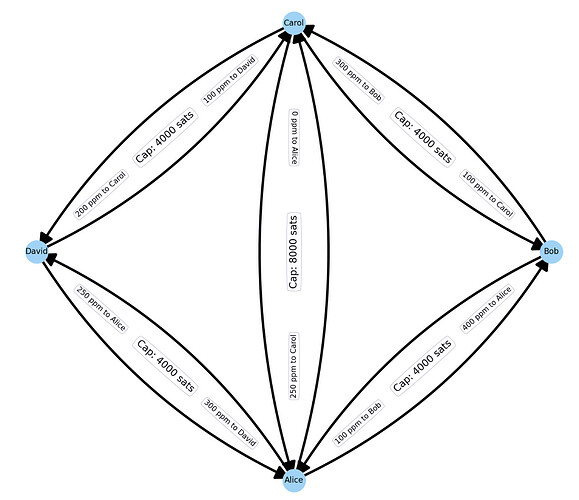
Take a look at the following extreme example:

Assume initially in the network every node has half of the capacity on their side and now nodes randomly send each other one sat.

The network will converge to the following state:

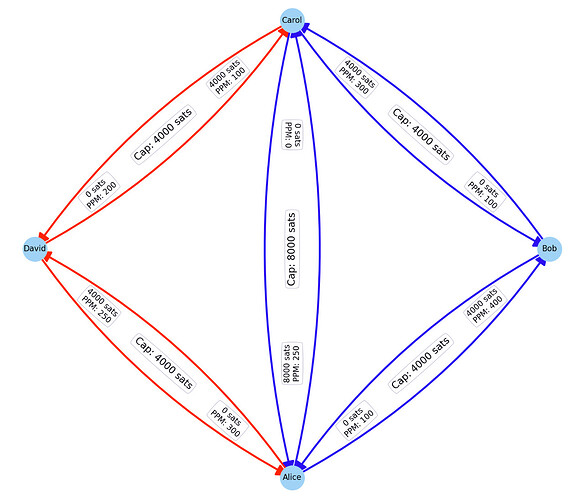
This is very interesting for several reasons:

1. All channels deplete (while all nodes keep roughly the same amount of total coins)
2. The red channels are those where the liquidity is on the cheaper end of the channel (contradicting your intuition that I have just created a “most expensive” spanning tree.
3. In fact, it is the global topology (including fees) and actual payment flows that defines which channels deplete (on which end)

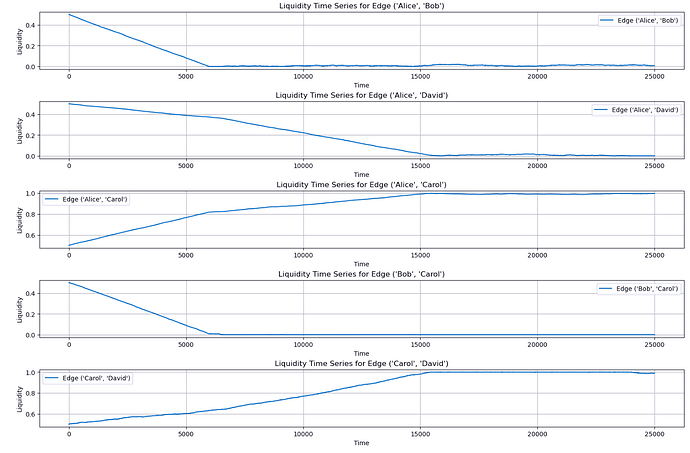
For completeness I will also post the time series of how the liquidity shifts in those channels while 1 sat payments are randomly conducted between the peers:

Again it is interesting to note that it is not the cheapest 0 ppm channel that depletes first. (Makes sense at it also has twice the liquidity) but in this particular case it depletes at the same time as the other channels.

@ajtowns

Are some nodes themselves running out of lightning funds?

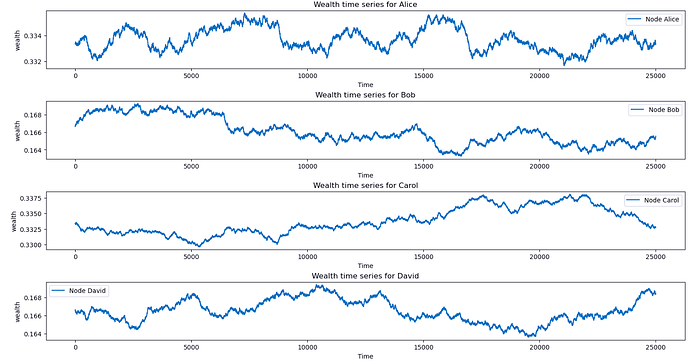
As just laid out, in the above example nodes have not run out of funds. I will add the zoomed in view depeicting how the wealth of each node progresses over time while the 1 sat payments deplete the channels:

Note if you zoomed the y-axis to [0,1] then you would visually just see streight horizontal lines.

Maybe I should have explicitely made the conclusion in my OP that:

• Channels deplete even if the netflow of all nodes is 0. No Source and Sink nodes are needed. Which I find quite remarkable and seems to be routed in the existance of cycles with varying costs.

@ajtowns

You could perhaps modify your simulation to address that, eg “I’m receiving $10000 a month, some by lightning, some by fiat rails; I’m likewise spending $9000 a month; if my lightning balance is $50000 or more, I’ll try to send all my payments via lightning; if it’s $25000, I’ll only try to send half my payments via lighting”.

If lightning is always your first choice when sending payments, then hitting a balance of $0 will mean as soon as you receive $50, you’ll send it right back out, so will stay depleted, which isn’t a good strategy if you want to get any value out of participating in lightning. The above might be a simple way of modelling a better one?

I am not sure about your proposed simulation. Of course I see the point that in reality people may chose between various payment rails and also onchain and ofchain payments and act acording to their liquidity requirements. But even in that world the LN graph is a somewhat closed system (with potentially less demand as some is taking place via other payment rails). In any case as laid out the phenomenon of channels to deplete seems to emerge because of various fees and the existence of cycles even if the netflow of all nodes in the network is 0.

Instead of focusing on such a mixed model wouldn’t it be more interesting to focus on how node operators should adjust their fees to help with flow control and adjust to channel depletion? Also Sending nodes could eventually adopt their route selection to use that knowledge to more quickly deliver payments.

@ajtowns

Having the network spontaneously resolve itself to an acyclic spanning tree seems similar to things like amoeba maze solving or electricity finding the path of least resistance to me.

Yes, the math that I use here to model and understand the emerging phenomena of the LN is also used to model electrical grids and other fluid networks. Intuitively it makes sense that it is also applicable in the amoeba maze solving (which I wasn’t aware of so far).