MUON has an interesting interplay here… x.com
Note that you still end up needing some sort of recursive proof inside R here. But MUON does the job of ensuring that no Tx Update can be broadcast without the right R being created for it, and makes Tx Update non-malleable.
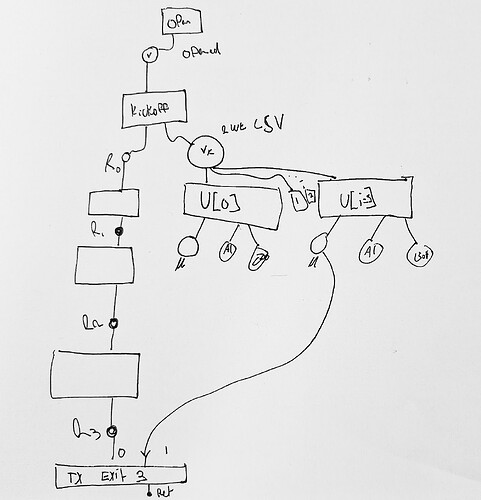
Describing the above graph:
Tx Open:
- Inputs: …
- Outputs: V_O ← N Sats
V_O.program ← tr(musig(A, B), {CTVHASH(kickoff) CTV})
Tx Kickoff:
- Inputs: V_O
- Outputs:
- R[0] ← 0 sats / dust
- V_K ← N Sats
V_K.program = tr(musig(A, B), {})
Updates are setup as follows:
Tx Update[i]:
- Sequence: 2 weeks
- Inputs V_K
- Outputs
- MUON X_i ← 0 Sats
- Alice ← k*N
- Bob ← (1-k) *N
Tx Ratchet i:
- nLockTime i
- Input R[i]
- Output
- R[i+1]
R[i]'s program:
tr(NUMS_H, { ratchet, cospend })
ratchet: <CTVHASH(Ratchet TX i+1)> CTV <musig(a,b)> CSFS [i] CLTV
cospend: 1 GETINPUT <COutpoint(MUON X_i)> EQUALVERIFY <CTVHash(Tx Exit)> CTV
Tx Exit:
- nSequence: 1 day (min time between last update?)
- Inputs: R[i] (via cospend path), MUON X_i
- Outputs: OP_RETURN Update[i].details_to_reconstruct
muon X_i.program: tr(NUMS_H, {<CTVHash(Tx Exit)> CTV 0 GETINPUT <R[i]> EQUALVERIFY })
How signing works:
First you open the protocol to create V_O.
Then you create the updates off of V_K (go ahead and sign – MUON X means a spend must exit).
You then create the ratchet update off of R, and exchange the sigs.
Note that you still end up needing some sort of recursive proof inside R here. But MUON does the job of ensuring that no Tx Update can be broadcast without the right R being created for it, and makes Tx Update non-malleable.