Dear fellow Lightning Network developers,
as some of you are already aware (through out of band communication) I am currently developing and finalizing a paper with a mathematical theory of payment channel networks. For the paper I created a small example that shows how to apply the rather technical and abstract geometric concepts to describe the Lightning Network. I thought this standalone example / application might be of interest for you.
The following is a summary of an ipython notebook from my Github reopository in which I develop the theory and research paper (Caution: The current latex file of the paper in the repository is a very early / incomplete and wrong draft. I would not recomand to read it yet. I expect a much more complete and accurate version to be updated later this month):
Abstract
In prior research we have provided a method of estimating the liquidity in payment channels. This was used to compute success probabilities for payments. The proposed model has several flaws:
- It assumes the liquidity distributions in channels are independent of each other
- it uses a uniform distribution to model the uncertainty
The second issue is being addressed through the introduction of bimodal models. However we believe the observed bimodal distributions emerge due to the geometry of payment channel network. This happens in particular if the first assumption is dropped.
Contribution
This notebook provides a tiny examples to demonstrate how one can compute the payment success rate between two peers on the lightning network for a payment amount even if no information about the liquidity distribution is availble. We do however assume that the sender owns more coins that he wishes to send (Though we could easily drop that assumption).
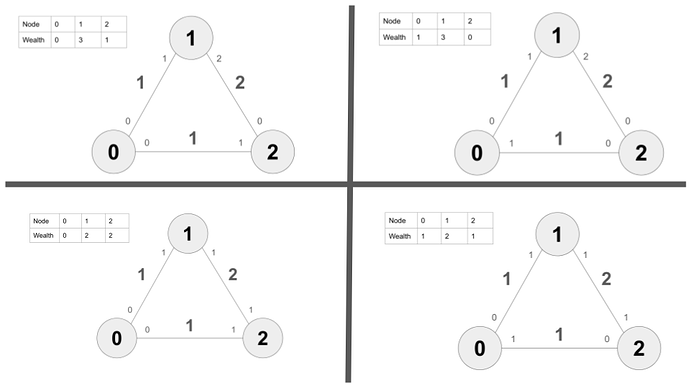
For this we start from the assumption that all feasible wealth distributions (not channel states!) in the given topology are equally likely to occur. As payments are changes in the wealth distribution we just have to test for all feasible wealth distributions if the change induced by the payment is still a feasible wealth distribution. The fraction of payments for which this is possible is the expected success probability of a payment.
Math formulation
Let w=(w_1,\dots,w_n) be a wealth vector. Furth let b_1,\dots,b_n \in \mathbb{Z}^n be unit base vectors that span the space of feasible wealth distributions. Then a payment is the new wealth vector w' which can be computed via the following:
w'= w -amt\cdot b_{src} + amt\cdot b_{dest}
if w' is feasible then the payment was feasible.
Caution this assumes that all feasible wealth distributions are equally likely. This is neither the same as assuming that the liquidity in channels is uniformly distributed nor the same as assuming that the wealth is equally distributed. The reason is that the network topology makes many wealth distributions infeasible. Thus despite assuming uniformity among the feasible wealth distributions this assumption is hopefully close enough to match the reality of a skew power law distributed wealth.
Important: The probabilities for a payment to be feasible is not related to attempt probabilities! Instead the probabilties computed with this method estimate weather it is likely that with sufficient attempts a payment is feasible and thus eventually succesfully being deliverd.
Results
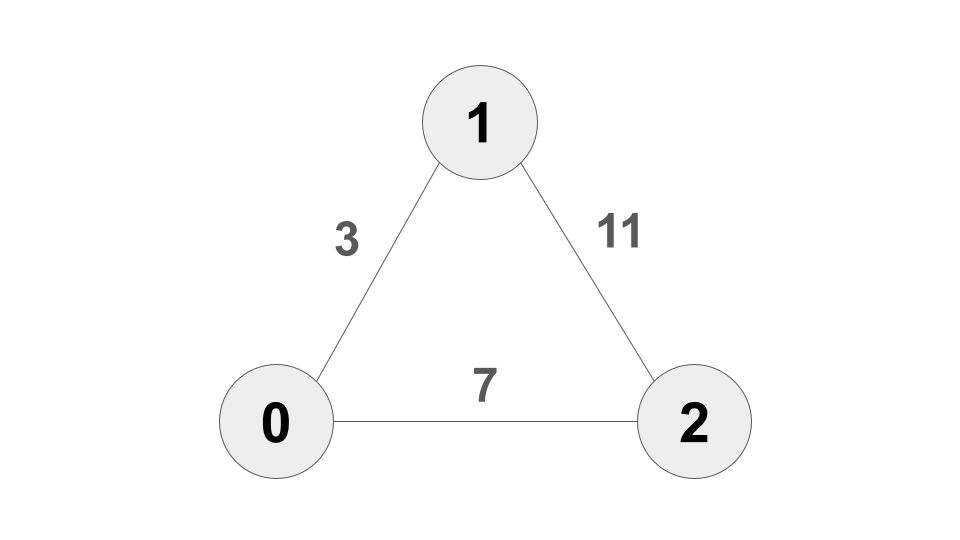
Take the following Network
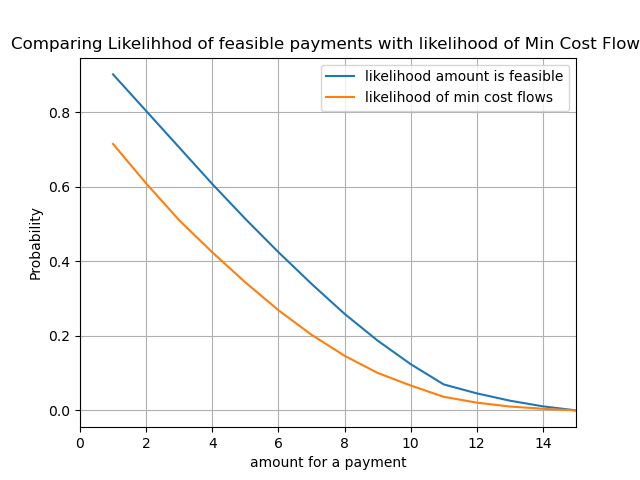
We get the blue curve that depicts how likely it is that a payment of a certain amount can be sent from any peer to any other peer. In comparison we depicted the likelihood of the min cost flow. Of course the min cost flow probability has to be lower as the payment could still be feasible while the min cost flow fails:
Example
Let us look at the likelihood of node 0 being able to send 5 coins to node 1. Given our methodology the likelihood that this payment is feasible on this network is: 39.22%
Using the methods of probabilistic pathfinding with independend and uniform liquidity distributions we see:
P1: s=0.00% (0)--- 3---->(1)
P2: s=21.87% (0)--- 7---->(2)---11---->(1)
This means of course node 0 cannot send 5 coins on P1 to node 1 as the path has only one channel with capacity 3.
The likelihood on the send path is 21.87%
The minmum cost flow would however split the payment and attempt to send coin along P1 and 4 coins along P2. This results in a 25% chance to settle this MPP attempt.
If on the other hand node 1 wanted to send 5 coins to node 2 then we get the following likelihoods:
5 coins from (1) to (2) expected success rate = 64.05%
P1: s=58.33% (1)---11---->(2)
P2: s=0.00% (1)--- 3---->(0)--- 7---->(2)
Not both P1 and P2 fail: 58.33%
MCF: s=43.75% 4 to P1 and 1 to P2
The increase makes sense as node 1 and 2 have access to more liquidity and thus should be more likeli to be able to conduct a payment.
Conclusion
We can produce a likelihood that estimates how likely a payment is feasible on the lightning network. We have seen that it is not necessary to estimate the liquidity in channels in order to do so. In particular there are always feasible states from which the payment is not feasible. (for example the receiving node doesn’t have sufficient inbound liquidity)
Thus Lightning Network payments cannot work in 100% of the time.
Also we have seen that optimally reliable payment flows always have a lower success probability than the probability that the payment is feasible. This is to be expected. However relying purely on flows and paths it seemed tricky to estimate the feasibility of a payment as one would have to simulate the payment loop.
Of course extending this method to a larger network is a bit more work as testing feasibility and sampling feasible wealth distributions is a bit more tricky (but possible in polynomial time as will be explained in detail in the paper)
I am curious about your thoughts, feedback or questions.
with kind regards Rene Pickhardt