Estimating Likelihood for Lightning Payments to be (in)feasible

[renepickhardt]

Thank you @stefanwouldgo for your thoughts.

1. I believe you know that I agree that the probability space of feasible payments and the space of likelihood for min costs flows are different.
2. I agree that my statement that the MCF probability has to be lower than the likelihood for a payment to be feasible this does not necessarily have to be true when various probability space are taken into account and I was probably a bit sloppy in my formulation (In which I only meant to be a requirement for theories to be sound)

That being said. I don’t think your counter example is accurate:

@stefanwouldgo

so overall there are 8 feasible wealth distributions.

If I have counted correctly we have 10 feasible wealth distributions (instead of 8):

| `node0` | `node1` | `node2` |
|---------|---------|---------|
| 0       | 1       | 3       |
| 0       | 2       | 2       |
| 0       | 3       | 1       |
| 1       | 0       | 3       |
| 1       | 1       | 2       |
| 1       | 2       | 1       |
| 1       | 3       | 0       |
| 2       | 0       | 2       |
| 2       | 1       | 1       |
| 2       | 2       | 0       |

@stefanwouldgo

Now let’s ask ourselves how probable is it that node 1 can pay 1 coin to node 0 as well as 1 coin to node 2. This is feasible whenever node 1 has at least 2 coins, node 0 has at most 1 and node 2 has at most 2. There are exactly 3 wealth distributions that apply: 121,022, and 031. So this is feasible with probability 3/8.

What about the distribution 130?

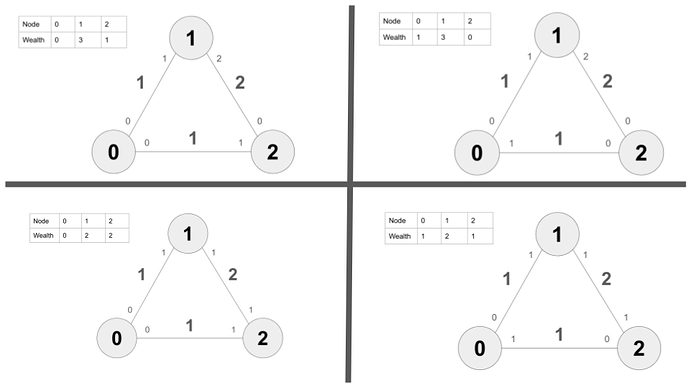
As seen in the following pictures I believe there are 4 feasible wealth distributions that allow node 1 to make a payment of 1 coin to both node 0 and node 2

→ thus we have 4 different wealth distributions that are feasible.

By the way, the only ones that occur twice and (and not three times) are: (1,1,2) and (1,2,1)

(Note: given that states with the same wealth distribution are created through circulations on the State Network and given the fact that the lowest capacity is 1 it makes sense that we can only find at most two different states with the same wealth distribution)

Thus accordingly in your example the likelihood that the payment is feasible would be 4/10 and not 3/8.

@stefanwouldgo

Now observe that there is only one flow that can achieve these two payments at the same time: 1 coin each directly from 1 to 0 as well as from 1 to 2. This is the min cost (=most probable) flow, and there are 5 network states where it will succeed (the same as the ones coming from the feasible wealth distributions above, but 121 is counted 3 times), So its success probability is 5/12, which is strictly greater than 3/8.

The mcf computation in my comparison does not start from network states! It takes the assumption from our paper in which we assume liquidity is uniformly independently distributed in each channel.

Additinally there are actually two flows that can achieve this payment that u describe:

1. The flow that you described (node1 sends 1 coin to node 0 AND node 1 sends 1 coin to node 2
2. The flow in which node 1 sends 2 coins to node 2 and then node 2 sends 1 coin to node 0. (Flow conservation is fulfilled here at node 2 because its demand is 1 and not 0)

according to the uniform probability distributions we get the following probabilities:

• Flow 1: 1/2*2/3 = 1/3 < 4/10
• Flow 2: 1/3*1/2 = 1/6 < 4/10

So indeed the flow that you picked was the MCF but according to the model that I was using to make the computation the probability of the attempt is 33.3% which is indeed lower that the likelihood that the payment is feasible (which according to my numbers is 40%)

To follow your flow computation: I only quickly counted how many feasible starting states exist and came to 4. I guess as the wealth distribution (1,2,1) should only be counted 2 times and not three times thay my quick counting is correct. However in that case the result would be 4/12 = 1/3 (surprisingly the same as my MCF model suggests) In particular this would not be a counter example.