Fastest-possible PoW via Simple DAG

Protocol Design
1

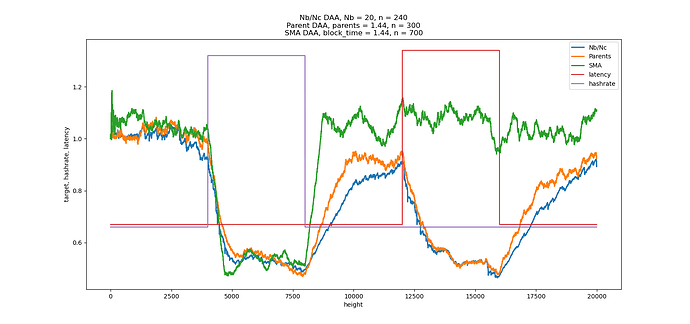
I was helping Bob McElrath on his difficulty algorithm for Braidpool and found a remarkable difficulty algorithm that doesn’t use timestamps, hashrate, or latency. Its goal is to be the fastest-possible consensus. Hashrate and latency independently create a wider DAG when they go up. But when you’re doing making it as fast as possible, hashrate * latency precisely cancels time units. You can simply set difficulty to target the DAG width.

Bob’s simple way of getting consensus is when the DAG width = 1 so that all nodes can agree what state the system was in. Width = 1 occurs when a block is the only child of the previous generation of blocks and the only parent of the next generation. This occurs when he’s the only block mined in 1 latency period after he sends it, and not block is mined in 1 latency period after everyone has received it.

But how do we measure DAG width? You just count your parents and target a fixed number of parents. This is an extremely simple idea compared to other DAG schemes that have to examine and think about a large tree of blocks.

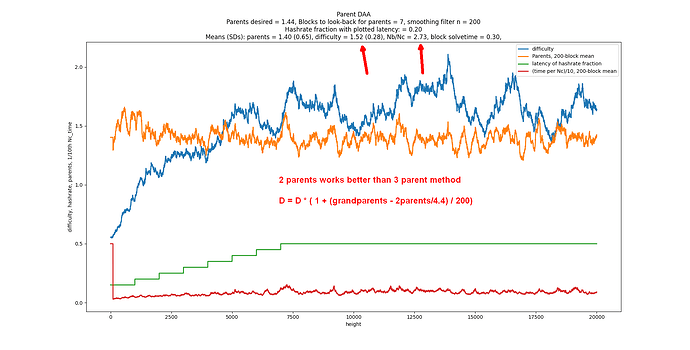
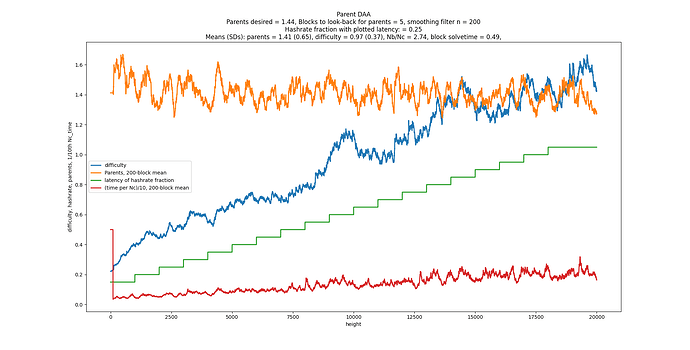
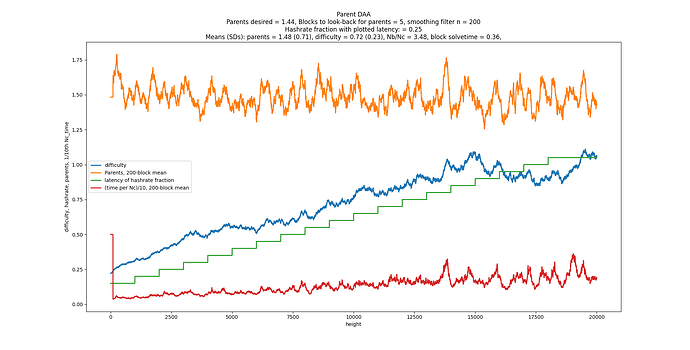
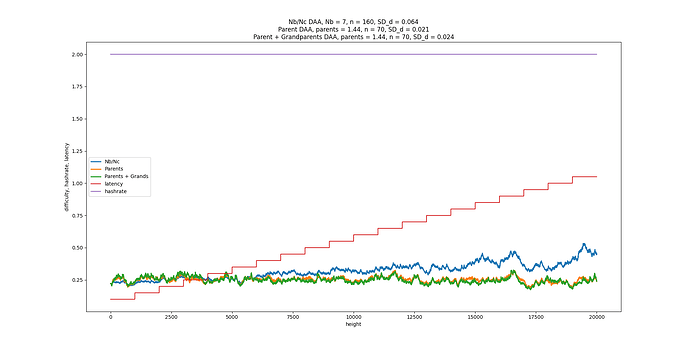
What the best number of parents? It turns out 2 gives the fastest consensus (i.e. the fastest time between 2 blocks at DAG width=1). When you target 2.000, the StdDev of number of parents is 1.000. But wait, there’s more. Consensus is achieved in exactly 2.71828x the latency, where latency is defined as the delay for all nodes in receiving a block. It’s 2x faster if you define latency as the median. Another interesting thing is that the ratio of total blocks to the consensus blocks is also 2.7182. Maybe someone could do the math to explain why.

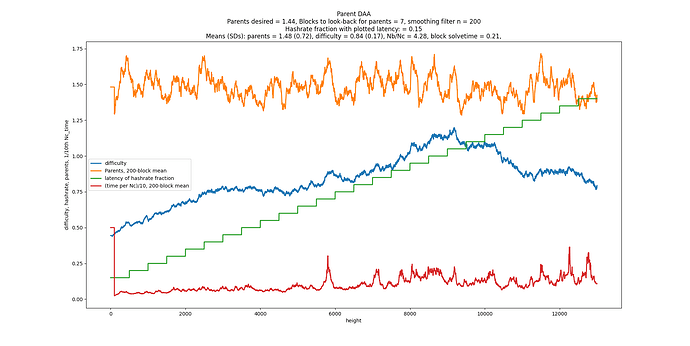
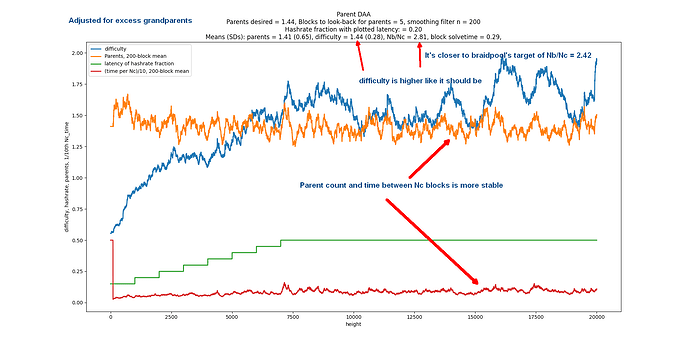
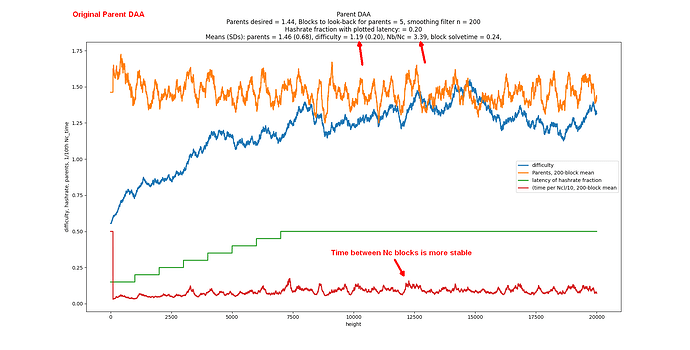
Here’s the DAA:

D = D_parents * (1 + parents/100 - 2/100)

if parents average > 2 in past 100 blocks, D goes up, and vice versa.

Here’s the command line output of my simulator below.


User chose to use 'a' as the exact latency between every peer.

=====   User selected parent-count DAA. =====
x = x_parents_hmean * ( 1 + desired_parents/n - num_parents_measured

median a	L	parents desired		n		blocks
1.00		1.0		2				500		50000
             Mean  StdDev
x:           0.995 0.030 (Try to get smallest SD/mean for a given Nb*n.)
solvetime:   1.006 1.008
Nb/Nc:       2.694 0.059 
num_parents: 2.004 1.007
Nc blocks: 18561
Time/Nc/a: 2.712 (The speed of consensus as a multiple of latency.)

DAG simulator by counting parents

Equivalence to Avalanche Speed and Efficiency: Basically, fees in both systems dictate how much “waste” you can spend on making it distributed and secure. Avalanche is so proud the number of messages/node doesn’t go up any as the number of nodes increases, but the network-wide waste in sending each other messages linearly goes up. Peers are basically “mining each other” with messages to get consensus. I don’t say mining here lightly. It’s very much the same level of waste for the same reasons with the same inefficiency. Network bandwidth is precious and expensive. PoW does local hashing to remove the need for network messaging. Fees determine how much waste either system has and fees => waste is the source of security and decentralization.

  • Avalanche <=> PoW
  • messages = hashes
  • more nodes = more hashing
  • stake = CAPEX in mining equipment
  • fast = this DAG
2

I’m not sure this is enough information for me to work out the entire scheme myself. Is there a forthcoming paper y’all are working on with this? It seems like a very interesting theoretical result even if it doesn’t have direct implications for a mainnet deployment (at least any time soon)

3

If you haven’t already, it might help to read braidpool/docs/braid_consensus.md at 6bc7785c7ee61ea1379ae971ecf8ebca1f976332 · braidpool/braidpool · GitHub

3 Likes
4

I don’t see how this approach could work in an adversarial environment – latency isn’t a global constant, it’s something that varies depending on who you’re trying to connect with, and it’s something that you can optimise for simply by colocating.

If you initially have 100% of hashrate colocated in a single data centre with a latency of 1ms, and then introduce a new miner located on the opposite side of the world with half the original hashrate (so ending up with a 33%/67% split), and a latency of 300ms to the original data centre, how does the difficulty adjust to take this into account? (Presumably increasing from X at 1ms per block, to about 450*X at ~300ms per block with +50% hashrate?) Does this work if the original miner (with 67% hashrate) just ignores all the blocks from the new miner while the new miner’s tip is more than K (6? 100?) blocks’ less work?

How would this algorithm behave in the interplanetary scenario, where 50% of hashrate is on earth, 50% is on mars, and the latency between the two varies between 3min and 20min?

If it works, it seems very nifty.

5

I used constant latency between all nodes to see pure results. I’ll answer in detail later. The simulator is coming out good. Here’s the response of different algorithms to 2x increases in hashrate and latency. The n values are filters to slow and smooth response (and in SMA its the actual averaging window, not a fliter). I chose them to give the same std dev in difficulty adjustment when hashrate is constant. Then the fastest response to changes is the best algorithm. Here SMA (simple moving average) won hashrate changes easily but is very time consuming to calculate in DAGs, and it has no awareness of latency changes. The Nb/Nc method counts bradpools “single block cohort” (Nc) in past 20 Nb blocks as indicated in the chart title. SMA has to go back 660 to 800 blocks instead. Bob will probably focus on the parent method since it’s so easy to calculate and is faster in responding. Notice parents= 1.44 for the parent method is the target instead of 2. I had an error in the simulation. 1.44 turned out best and proved equivalent to Bob’s Nb/Nc = 2.42 method backed by his derivation. 2.42 = 1+1/Q where Q solves 1/Q = Q * e^Q

17356923948868316595468585569479
173569239488683165954685855694791585×746 88 KB

6

This reminds me somewhat of research by (I believe) Andrew Miller (though I fail to find a reference right now) from around 2012 or so, where he suggested a consensus mechanism that (by using DAG structure) has difficulty adjust not based on hashrate, but based on percentage of blocks not included in the main chain. So there would be a target percentage of wasted (“orphaned”) blocks, and if the real percentage is too low, the difficulty would decrease, and if it was too high, it would increase. The idea is that the percentage wasted blocks determines the advantage a colluding attacker has against honest miners, so if we accept a fixed small percentage, the block rate should be as high as possible while staying below that fixed percentage.

However, I think it suffers from the same problem pointed out above, that it incentivizes changing the network topology to colocate miners.

7

Here’s a chart showing the problem. All DAG’s must not accept new parents who have parents that are “too old”. Consensus is formed because (and when) when you stop letting in those ‘old’ blocks. As a result of having a cut-off, there can be forks where PoW will decide the winner.

The chart below uses a cut-off, but not exactly like the above because it assumes all miners are honest. The DAA does a “look-back” of only 7 blocks to have a fast consensus. In this example, 15% of the hashrate has an ever-increasing latency indicated by the steps (this has the same effect as if 85% of hashrate had a decreasing latency). Since the network hashrate is constant, when the difficulty starts dropping (instead of increasing with average latency due to the 15%), it’s the result of those high-latency miners producing blocks the DAA can’t see (they’ll be orphaned). It thinks the hashrate is lower.

image
image1923×965 128 KB

I may have a solution, or partial solution. Instead of (only) looking at parents. I can base the DAA difficulty on a count of grandparents and maybe great-grandparents. If a parent block cites as his parent(s) what other parents (his “siblings”) are calling grandparent, that block has a higher probability of having a higher latency than his siblings. It doesn’t occur often if everyone has the same latency, so I can increase difficulty a lot when it happens and it has little average effect, but if it happens more than expected due to miners with a much higher latency than the average, it can have a large effect. In other words, if the statistics that assume everyone has the same latency are being violated, it gives an increased difficulty which benefits the slow miners by slowing down block time (while not changing the look-back block count) so that they don’t fall outside the “look-back” window. It gives less incentive to get your latency below the average while still incentivising everyone to get lower latency, if they want more blocks per real time.

8

Zawy used a constant ‘a’ in his simulations but in my simulations and in practice ‘a’ is measured by the average “width” of the DAG: Nb/Nc which is the ratio of beads (share-chain blocks) to the number of total-ordered consensus “cuts” in the graph (aka “cohorts”). @sipa this is exactly a difficulty adjustment based on “blocks not in the main chain”, I’m just using some more graph theory to describe the same concept. If you could dig up that reference (probably related to HoneybadgerBFT?) I’d appreciate it and will credit Andrew.

Zawy’s observation is that if you write the bead time and cohort time in units of ‘a’, (Tb/a and Tc/a) you’re left with a function of only one dimensionless variable axlambda where x is the target and lambda is the hashrate. This gives us a clock-free way to do retargeting by targeting having the most possible graph cuts (global consensus points). This is pretty cool because it eliminates a lot of timewarp and DAA manipulation games.

The doc @harding linked above is a work in progress and doesn’t yet include this observation. You can see my first stab at this there which is MUCH more complicated than targeting either a fixed number of parents or a fixed Nb/Nc (which seems to be equivalent).

As far as not punishing latency, the algorithm will pay miners proportional to their work as long as their latency isn’t excessive. At high latencies the miner is likely to create Bitcoin orphans and reduce the profit of the pool. So we need to incentivize latency all a level similar to bitcoin’s natural orphan rate, but if we further incentivize latency below the natural propagation time of shares, we’re incentivizing geographic centralization. High latency corresponds to large cohorts, and for cohorts over a certain size (probably around 25 beads) I want to sort the beads “farthest” from the highest work path through the cohort, and start dropping the highest latency beads from the payment pool. Bitcoin’s orphan rate is around 1% so rough numbers: a=250ms, so a 25 bead cohort corresponds to 5-6s and corresponds to the orphan rate. This deeply assumes all miners are on planet earth and edge cases exist which will use a minimum allowable latency that corresponds to the size of the earth. We’re not offering a solution for mining on the moon. With 3s additional round trip to the moon, mining on the moon is marginal when considering bitcoin’s orphan rate, but mining in Mars is impossible. This should not incentivize geographic centralization. (On earth)

The above idea is contrary to Zawy’s suggestion to orphan high latency beads, I want to include them but not pay them.

9

The only difference I can see in what @sipa described and what I’m doing is that they wanted a small percentage of orphans. By targeting a number of parents (1.44), I’m targeting a percentage of blocks that would have been orphaned (44%).

I think Bitcoin’s orphan rate is about 0.04% to agree with the orphan estimate of e^(-latency/600).

10

Adjusting for “excess grandparents” as described above seems to have potential in alleviating the topology problem (“latency inequality”). The idea is that high-latency miners will disproportionally reference a parent that is a grandparent of a low-latency sibling. I did some data collection and noticed these “grandparents” occur equally as often as 3 parents when my target is parents = 1.44 and when the latencies are evenly distributed. The grandparent to 3-parent frequency ratio is normally 1:1 and it increases when latency is higher for some of the miners.

To clarify, I want to identify blocks that have a parent that would have been a grandparent if not for the block having excessive latency in receiving the parent and/or sending out his own block that’s a child to it. I’m calling them a grandparent, but they’re a parent. I adjust the DAA for the child block. He’ll get very slightly higher difficulty for having longer latency and thereby having this type of parent, and his descendants will feel the small effect. We assume >50% honest miners who won’t steal pennies to lose pounds.

Data collection to see if it would have the effect I thought it would

naughty grandparents per 3-parents
hashrate fraction v. multiples of latency increase
HRF		2x			4x			8x
0%		102%		102%		102%
1.25%	108%		111%		100%
2.5%	111%		121%		94%
5%		117%		134%		93%
10%		131%		169%		126%
20%		147%		195%		215%
30%		140%		192%		229%
40%		133%		179%		206%
50%		124%		153%		188%
60%		117%		138%		174%
70%		116%		127%		169%
80%		108%		120%		165%
90%		107%		117%		159%
95%								149%
100%	102%		102%		102%

Since the ratio is 1.02 during equitable latency conditions, a simple change to the difficulty algorithm could be used. The existing difficulty was:

D = avgD * (1 + (numParentsObserved - 1.44) / 200 )

so I added:

D = D * (1+ (grandparents - 3parentsBoolean) / 200 )

avgD is the average difficulty of the block’s immediate parents. 3parents is either 1 or 0 depending on if there were 3 parents for that block or not. It could be more sophisticated. These type of gandparents can be more than 1 for a block.

It worked as good as the original equation under normal stable conditions and during hashrate attacks without change.

These two charts show it reduced the problems caused by 20% of the miners having up to 4x slower latency.

image
image1920×975 131 KB
image
image1920×975 127 KB

A comparison to 1 or 2 parents has more data and thereby be more accurate. 2 parents gave the best result. An adjustment to the 2nd equation is needed due to 2 parents being 4.4x more common than ‘grandparents’ under homogenous latencies. To clarify “hogobenous”: latencies can vary widely and randomly and everything works fine for all algos as long as the latency is homogenous among all miners. The grandparent adjustment has a beneficial effect when they aren’t

D = D * ( 1 + (grandparents - 2parentsBoolean/4.4) / 200)

image
image1920×975 126 KB

It doesn’t work as good if the hashrate fraction is 15% instead of 20%. It would be good to provide protection when only 5% of miners have excessive latency, but that seems too challenging.

The next 2 charts show the benefit is more pronounced when 25% of the hashrate has high latency. The 1st one with the higher difficulty is with the new equation above.

grandparentsF
grandparentsF1920×975 137 KB

grandparentsG
grandparentsG1920×975 129 KB

11

The Nb/Nc DAA doesn’t have any problem with differences in latency topology. Even if only 5% of miners have up to 20x higher latency, and if the DAA looks back only 7 blocks (just as fast as parent method), they throw off everyone’s ability to form a “consensus cohort” . It automatically sees they are referencing a lot of grandparents and great grandparents. This keeps the difficulty high and it stays close to the ideal Nb/Nc = 2.42 ratio (Parents = 1.44/block). At 5%, the grandparent method isn’t any better than the parent method. The difficulty doesn’t rise as high in this chart compared to the others because it’s only 5% of the hashrate .

Figure_1
Figure_11920×975 73.6 KB

12

I’m fairly skeptical of using graph structure alone and the DAA here to handle high latency. High latency is already observed and accounted for using the Nc/Nb method (because high latency generates large cohorts). I don’t want to create incentives for miners to do anything other than naming all known tips. So, I think we need to pull in another timing measurement to decide whether beads have abnormally high latency or not. Remember that just due to the statistics of the Poisson distribution, large cohorts and excessive grandparents will naturally be generated some calculable fraction of the time, and doesn’t represent a problem for the system or evidence of an attack. Adjusting the difficulty due to these infrequent large naturally-occurring cohorts biases the difficulty algorithm relative to the naive Nb/Nc=2.42 algorithm.

Let me elaborate on my alternative here where instead of adjusting the difficulty, we will decide to not pay high-latency beads.

First, assume that Braidpool commits to a millisecond resolution timestamp in its committed metadata that we will use. Second, consider the following diagram of a high-latency bead:

       /-------o---------\
  o-o-o                   o-o-o
       \o-o-o-o-o-o-o-o-o/

Where the bead on the top has high latency and the chain of beads on the bottom is the “highest work path” through the DAG. This is the most common example of what a high latency bead will do the DAG. In its absence you’d just have the chain on the bottom. The lower chain will in general have higher order structures and e.g. Nb/Nc=2.42 if we ignore the high latency bead. This example does not have excessive grandparents.

A good measure of latency of any bead is:

bead_latency = median({t_c}) - median({t_p})

where {t_c} is the set of the timestamps of children, and {t_p} is the set of timestamps of parents of that bead. This measure has the advantage that it is not influenced by the miner’s own timestamp, only by timestamps reported by other miners, so is very difficult to game. A miner also doesn’t know what his own latency will be until children of his bead appear, so it’s in his best interest to broadcast his bead as quickly as possible, to collect those children.

We want to pay everyone “close” to the main highest-work path and not pay the high-latency bead here. We also don’t want the presence of the high-latency bead to affect other miner’s rewards, as this constitutes an attack vector. Therefore the simplest thing to do is have a hard cutoff on bead_latency, probably around 5s, above which the bead won’t receive a reward. We can allow cohorts to be as large as necessary to include all known beads without orphans/stale beads, so as to get an accurate measure of global latency, even if an extended network split occurs, and without biasing for rare but naturally-occurring largeish cohorts.

This means:

  1. The DAA is using a as its (only) timing measure through Nb/Nc
  2. Payment decisions are using other miners timestamps

@zawy has been killing it with his simulations over the holidays, but I’ll present some similar simulations soon now that the holidays are over :wink:

P.S. if you want to discuss this in real time, join our Braidpool Discord

1 Like
13

As an aside, fully validating a DAG chain is quite difficult with the current Bitcoin Core architecture. The benefit of fully validating weak blocks is that it lets you safely distribute rewards weighted by fees, using a scheme similar to PPLNS with job declaration

It has to update its UTXO set database at every block. If there’s multiple branches it would need to keep a cache around for each branch. And it needs to store each cache on disk on shutdown. It would also need to track multiple copies of the mempool, at least if it wants to process new blocks as quickly as possible.

Interestingly a Utreexo based node won’t have this problem. Its UTXO set is a tiny 1kb Merkle forest. The node can store a copy along with every block so there’s almost no overhead for tracking multiple branches.

Multiple mempool branches might still be problematic though, not for storage but because it’s computationally expensive to update. Though perhaps with cluster mempool that’s not a problem either.

I would imagine that Libbitcoin can also handle a DAG structure more easily because of its different architecture, see e.g. Libbitcoin for Core people

14

Thanks for the input @sjors – I’m aware of these issues and am planning to use deterministic block templates, as described here.

Each bead (share-chain block) will be able to add bitcoin transactions to a “committed mempool”. From there we will use a deterministic algorithm to select from this committed mempool (e.g. “highest fees” or “lexical ordering on txid”). This way we don’t need to propagate transaction or block template data in shares, as it can be computed independently by all nodes. We don’t have to actually update the UTXO set though, since most shares are not bitcoin blocks.

Yes this means each bead has its own mempool, though most transactions will be shared among them. So we need to be able to do a fast diff/merge between the mempools of different beads.

We’re going to have to deeply investigate the cluster mempool and thanks for the UTreeXO pointer, I’ll take a look. Contributions welcome :wink:

If we have to write our own UTXO management code instead of calling bitcoind…then that’s just what we’re going to have to do. I’m a big fan of libbitcoin’s approach and will emulate it as much as possible.

15

I think it would be interesting to analyse this both as a difficulty adjustment for a standalone consensus system (as if bitcoin didn’t exist), and as its intended purpose as a way of coordinating reward sharing for bitcoin mining. I think those scenarios are a bit different – for example some form of 50% attack on the former is probably catastrophic, but the same “50% attack” on the latter as long as its kept at the pool level, even when completely successful, can just be dealt with as “okay you’re not letting us in your pool, so we’ll make our own pool” and be completely fine.

In particular, if you have 10% of bitcoin hashrate in a single data centre, and it all uses a single pool with 1ms latency, and meanwhile 70% of hashrate is distributed evenly around the world at 300ms latency on average, then just having two braidpools that run independently is likely fine for everyone concerned. But if the braid were the thing people were trying to come to consensus on diretly, then a chain/braid split isn’t an acceptable outcome.

0.04% (one every 2500 blocks) seems roughly accurate based on fork.observer’s reports. I think the orphan rate due to network latency estimate is 1-e^{-a/600} so at 0.04% that gives a latency of a \approx 240 milliseconds which seems plausible, presuming the only orphans we actually observe are due to latency.

With the same latency applying to a global braidpool, but an expected block rate of 100 blocks per ten minutes (10% hashrate at 1/1000th of the difficulty), then the expected “orphan” rate is about 4%. Conversely, if you target an expected “orphan” rate of 44%, with 10% hashrate, that means beads are 14,500 times easier than blocks, rather than 1000 times easier?

I think/conjecture the look-back/latency constraints are probably critical for this approach’s ability to come to consensus between subsets of hashrate with very different latency properties – the 200:1 latency ratio I suggested would (I think) make it difficult for the latest beads from the two groups to have sufficiently common ancestry that they get merged; whereas I’d expect a 2:1 latency ratio to be more-or-less fine.

If there’s a latency ratio limit where good behaviour breaks down, I think that would be interesting to understand, even if the result is just “well, we automatically have two distinct braid pools in that case, which each pay their members out fairly from the bitcoin rewards for that pool’s found blocks”.

That sounds a bit exploitable to me (presuming including them means they contribute to the most-work comparison) – if you’ve got a signfiicant portion of hashrate, just artificially declare delay everyone else’s beads by X milliseconds, before you include them in your braid. Every now and then everyone else will have a run of bad luck and your tip will become the best tip, making their work not result in a payout. Perhaps the feasibility of this depends on the relationship between X and when payouts get finalised.

16

I’ve moved this into Protocol Design, and added a braidpool tag.

1 Like
18

This is what I’m doing. Braidpool’s specifics aren’t on my mind yet.

Nb/Nc = 2.42 (approx parents = 1.44) results in solvetimes 2.9x mean latency if latency varies randomly from 0 to 2x the mean. It’s independent of hashrate. It targets a solvetime in units of latency, but affected by latency distribution. So if mean latency in a Braidpool = 0.5 seconds, block time is 1.45 s, 417 blocks in 600 s. At 10% hashrate, that’s 4,000x easier.

Using 1-e^(-0.5/1.45), I get a 29.2% orphan rate for Nb/Nc = 2.42 and a uniformly random latency variation around that mean. This equation for orphan rate is approximate. There’s a paper from way back that derives something precise. Looking at it another way, 1/2.42 is the fraction of blocks without any sibling according to any parents or children. If half the remaining 1.42 blocks would have been orphaned then 0.71/2.42 = 29.3% orphan rate.

To me, “not paying them” = orphaning, whether or not they’re included in the DAA calculation.

The Nb/Nc DAA doesn’t seem to have any problem with widely-varying latency. For example, if 5% have 200x longer latency, the solvetime per latency is still in the 2 to 3 range. The Nb/Nc DAA is pretty incredible at how well it handles topology and random variations in latency.

I was adjusting the difficulty based on “parents who were supposed to be grandparents” only because the Parent DAA needed it.

The statistical problem of accidentally not rewarding also applies if you use a hard 5 s limit: there could be a natural network delay and you don’t want to enforce a 5 second limit if half the miners are having that kind of delay, or if they’re unlucky and it’s taking 5 s to find a solution. The only way to determine that you’re not having either problem is to confirm there was a sufficient number of other blocks in that time. This is just a great grandparent check that might be able to be used instead. (The “great grandparent method” is not rewarding a block if he sees a parent that all his siblings see as a great grandparent.) Are the timestamps needed or are both be useful? The time limit check has false positives on slow blocks while the great grandparent method has false positives if they’re too fast.

Using a >= great^4 grandparent rule never has a false positive if latency is a uniform distribution. This is at the 5 s level when median latency = 0.25 s. If 10% of the hashrate has 4x the median, there’s a false positive on 2% of their mined blocks. At 10% with 10x latency, it’s 15%. 10x latency is at 2.5 seconds so they aren’t far from not meeting the 5 s limit. But 0.1% hashrate with 40x latency (10 s) has only 35% of it’s blocks rejected. So a combination of the two methods might be good.

19

Sounds like you might refer to

Miller, Andrew, and Joseph J. LaViola Jr. “Anonymous byzantine consensus from moderately-hard puzzles: A model for bitcoin.” Available on line: Anonymous Byzantine Consensus from Moderately-Hard Puzzles: A Model for Bitcoin | Satoshi Nakamoto Institute (2014).

1 Like
20

I asked Andrew. Apparently it was just a bitcointalk post post, and later referenced in the NC-Max paper.

1 Like