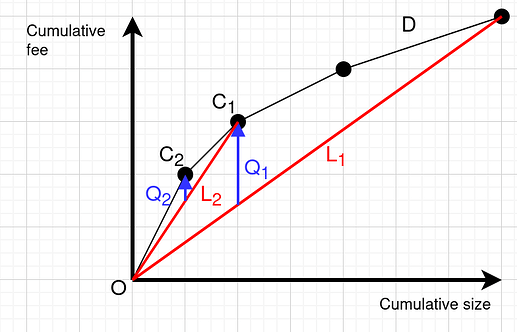
To demonstrate what I mean above:
- D is the feerate diagram of the optimal linearization, so each black dot on it corresponds to some topologically-valid subset, and D is the convex hull through them. The vertices of the convex hull (and the transaction sets they correspond to) are what we are trying to find.
- L_1 is the line whose slope is the \lambda_1 for the first min-cut iteration, corresponding with the feerate of the entire cluster.
- Then we run the min-cut algorithm, to find the closure C_1 whose weight Q_1 = \operatorname{fee}_{C_1} - \lambda_1 \operatorname{size}_{C_1} is maximal.
- Then we set \lambda_2 to the previous solution, i.e., \lambda_2 = \operatorname{fee}_{C_1} /\operatorname{size}_{C_1}.
- L_2 is the line whose slope is \lambda_2.
- Then we run the min-cut algorithm again, to find the closure C_2 whose weight Q_2 = \operatorname{fee}_{C_2} - \lambda_2 \operatorname{size}_{C_2} is maximal.
In every iteration, one or more chunks are removed, but the solutions each correspond to a prefix of chunks of the optimal linearization. So by the time we find the first chunk C_2, we have found the next chunk already too (C_1 \setminus C_2), but not the one after that because the first iteration skipped that one already. I’m guessing that’s where the contraction comes in: replace the source s with C_1 \cup \{s\}, and start over, and somehow that is still possible without fully resetting the algorithm state?