New attempt, with a fully “geometric” approach to show the new diagram is above the old one, but largely using insights about sets from @ajtowns’s proof sketch above.
Theorem
Given:
- A linearization L
- A topologically valid subset G of the transactions in L (“G” for “good” transactions).
- Let L_G be the linearization of the transactions G, in the order they appear in L.
- Let L_B be the linearization of the transactions not in G (“bad”), in the order they appear in L.
- Let f be the highest chunk feerate of L.
- L_G (considered in isolation) must form a single chunk, with feerate \geq f.
Then:
- L_G + L_B is at least as good as L (better or equal feerate diagram, never worse or incomparable).
Let’s call this the gathering theorem (it matches what the VGATHER* AVX2 x86 CPU instructions do to bitsets).
Proof
- Let S(x), F(x), R(x) respectively denote the size, fee, and feerate of the set x.
- Let (c_1, c_2, \ldots, c_n) be the chunking of L (the c_i are transaction sets).
- We know R(c_i) \leq f for i=1 \ldots n, because of input assumptions.
- Let \gamma_j = \cup_{i=1}^{j} c_i (union of all chunks up to j).
- Let e_i = c_i \cap G for all i=0 \ldots n (the good transactions from each chunk).
- Let \zeta_j = \cup_{i=j+1}^{n} e_i (union of all good transactions in chunks after j).
- Because \zeta_j is a suffix of L_G, which is a single chunk with feerate \geq f, we know R(\zeta_j) \geq f for all j=0 \ldots n-1.
- Let P(x) = (S(x), F(x)) be the point in 2D space corresponding to the size and fee of set x.
- Let D be the diagram connecting the points (P(\gamma_j))_{j=0}^{n}, corresponding to the prefixes of chunks of L. This is the diagram of L.
- Let N be the diagram connecting the points (0,0) followed by (P(\gamma_j \cup \zeta_j))_{j=0}^n, corresponding to the prefixes of L_G + L_B consisting of all good transactions and the bad transactions up to chunk j.
- N is not the diagram of L_G + L_B because that requires rechunking that linearization. However, rechunking can only improve the diagram, so N is an underestimate for the diagram of L_G + L_B.
- D is a concave function. A point lies strictly under a concave function iff it lies under every line segment that makes up D, extended to infinity. Thus, a point lies on or above D iff it lies on or above at least a single line that makes up D.
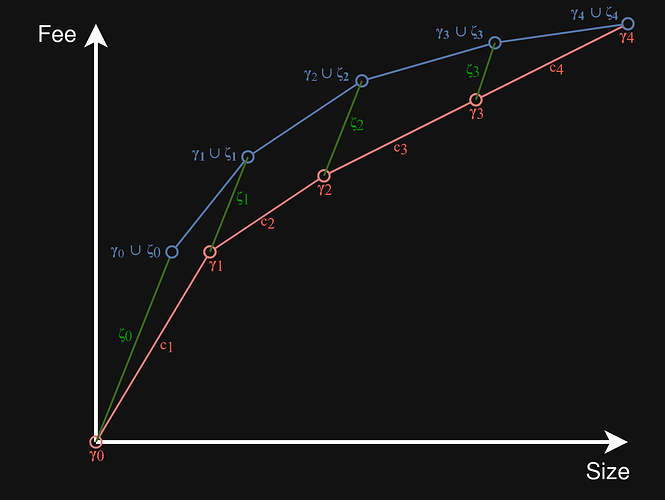
In the drawing below, the blue diagram formed using the \gamma_i+\zeta_i points (plus initial green \zeta_0 segment) is an underestimate for N, the diagram of L_G+L_B. The red diagram shows D, the diagram for L. Intuitively, the blue diagram lies above the red diagram because the slope of all the green lines is never less than that of any red line:
In what follows, we will show that every point on N lies on or above a line making up D. If that holds, it follows that N in its entirety lies on or above D:
- The first diagram segment of N, from (0,0) to P(\gamma_0 \cup \zeta_0), is easy: it corresponds to L_G itself, which has feerate (slope) \geq f. All of these points lie on or above the first line of D, from P(\gamma_0) (= (0,0)) to P(\gamma_1), which has feerate (slope) f.
- For all other diagram segments of N, we will compare line segments with those in D with the same j = 0 \ldots n-1. In other words, we want to show that the line segment from P(\gamma_j \cup \zeta_j) to P(\gamma_{j+1} \cup \zeta_{j+1}) lies on or above the line through P(\gamma_j) and P(\gamma_{j+1}).
- P(\gamma_j \cup \zeta_j) lies on or above the line through P(\gamma_j) and P(\gamma_{j+1}) iff R(\zeta_j) \geq R(c_{j+1}). This follows from R(\zeta_j) \geq f and R(c_{j+1}) \leq f.
- P(\gamma_{j+1} \cup \zeta_{j+1}) lies on or above the line through P(\gamma_j) and P(\gamma_{j+1}) iff R(c_{j+1} \cup \zeta_{j+1}) \geq R(c_{j+1}). This follows from the f relations too, except for j=n-1, but there the endpoints of the two graphs just coincide.
- All points between P(\gamma_j \cup \zeta_j) and P(\gamma_{j+1} \cup \zeta_{j+1}) lie on or above the line through P(\gamma_j) and P(\gamma_{j+1}), given that the endpoints of the segment do.
Thus, all points on an underestimate of the diagram of L_G + L_B lie on or above the diagram of L, and we conclude that L_G + L_B is a better or equal linearization than L.
Generalization
It is easy to relax the requirement that L_G forms a single chunk. We can instead require that only the lowest chunk feerate of L_G is \geq f. This would add additional points to N corresponding to the chunks of L_G, but they would all lie above the existing first line segment of N, which cannot break the property that N lies on or above D.