Propagation Delay and Mining Centralization: Modeling Stale Rates

Protocol Design
1

A few months ago i posted a detailed analysis of Selfish Mining. “Selfish” Mining is a strategy whereby a sufficiently large minority miner can maximize its revenues by selectively publishing blocks. While it’s interesting to consider what is the optimal strategy a miner could adopt in this simplified model, i think it’s primarily interesting in demonstrating the considerable extent to which longer block propagation times advantage larger miners. Following up on this, i looked into how propagation time affects a miner’s revenue as a function of its hashrate.

In order to make this tractable, let’s consider a simplified model whereby all propagation time is uniform and all miners are using the regular mining strategy (when a block is found, start mining on top of it immediately, publish it immediately, switch to mine on a valid chain with more PoW as soon as it’s received). Essentially a star network topology whereby the Bitcoin p2p network serves as the hub:

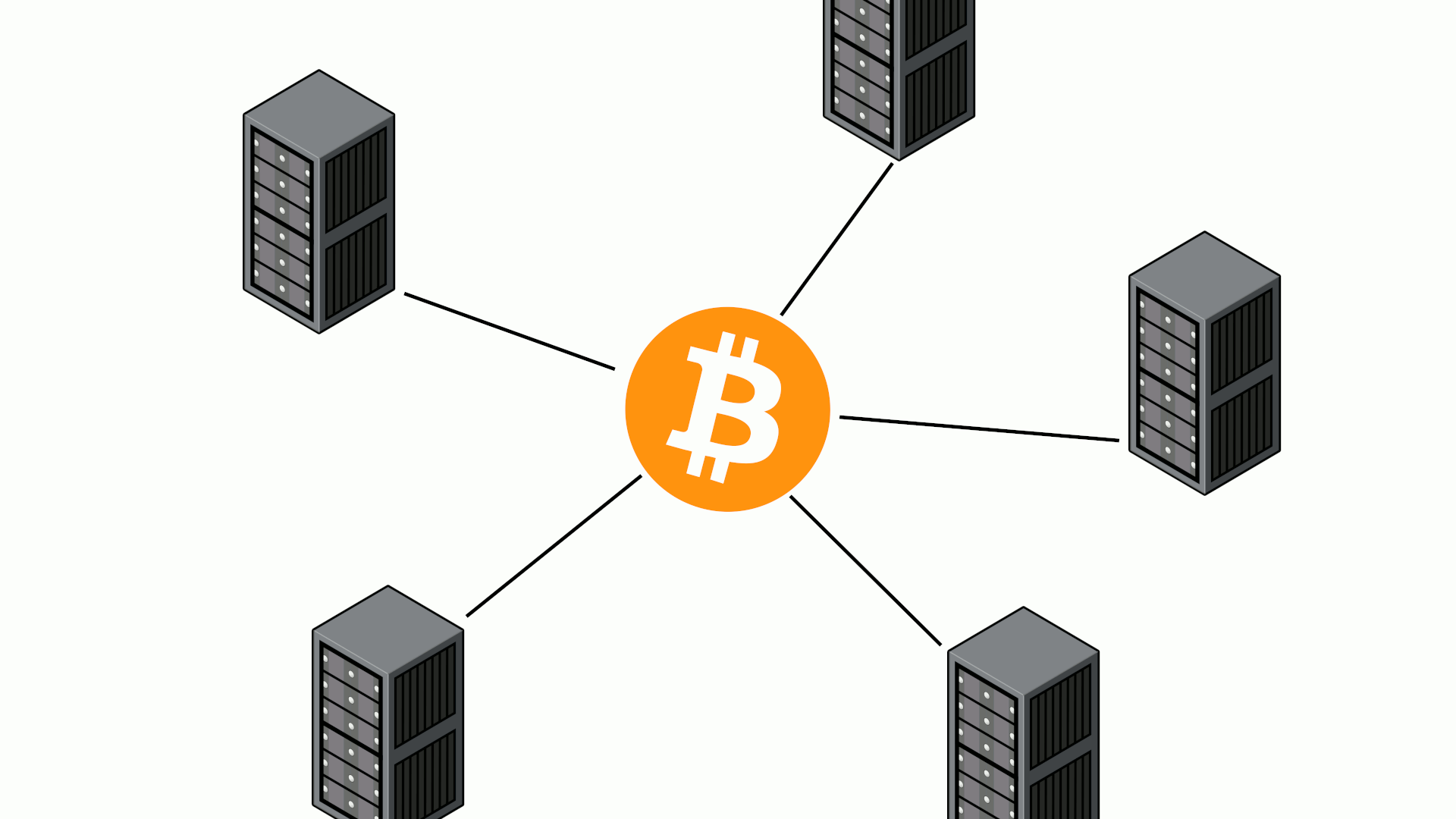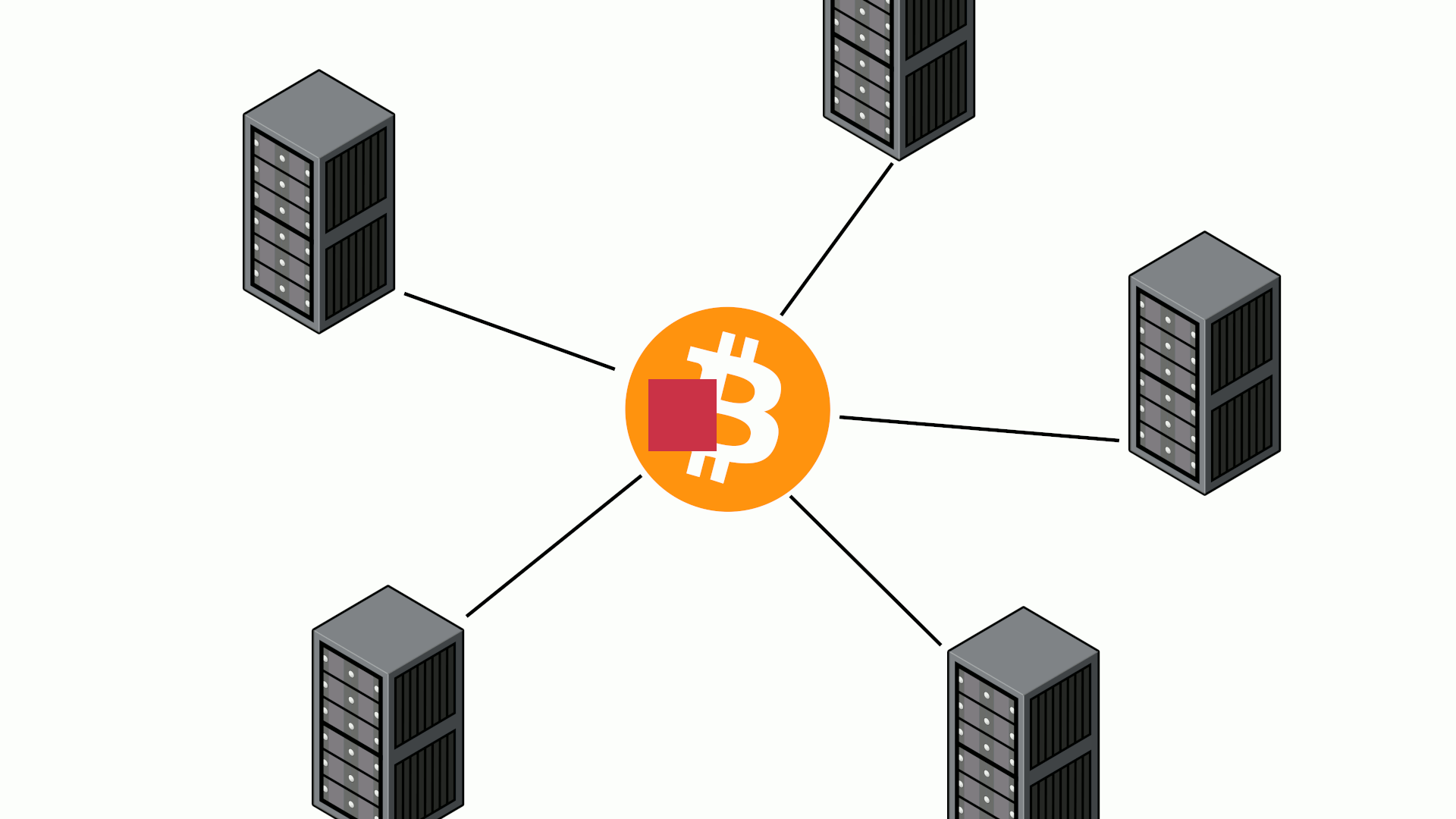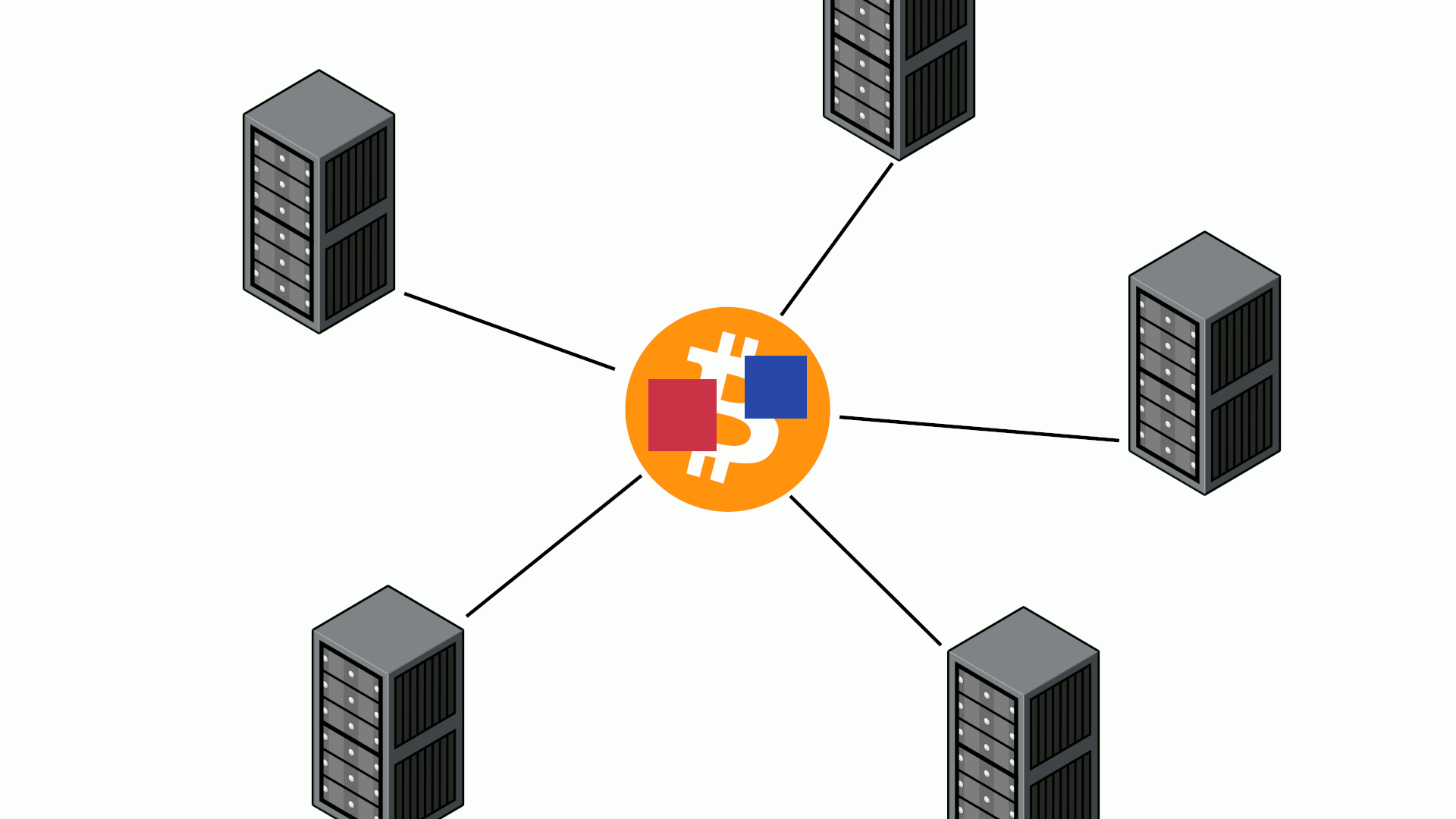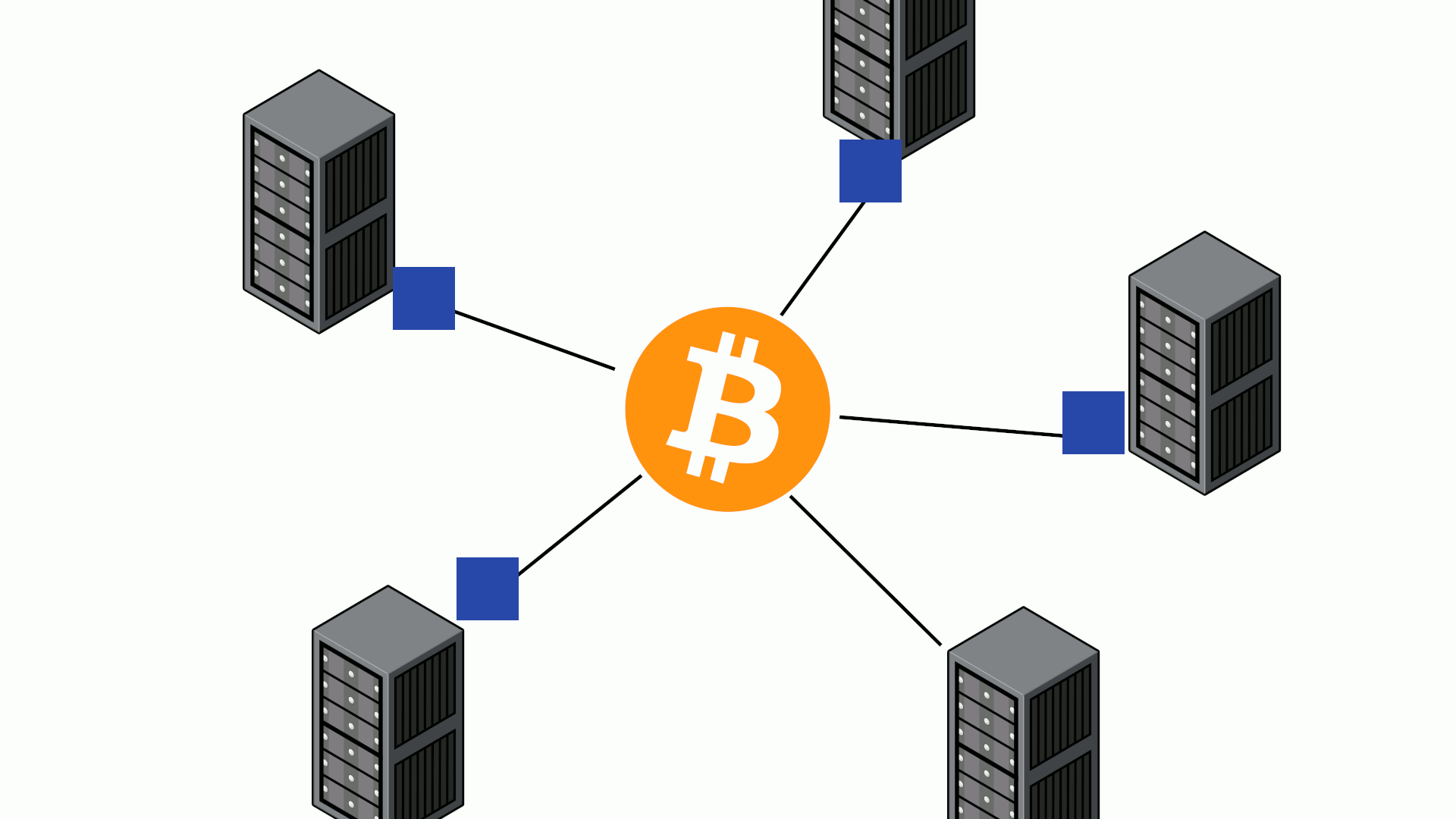
miners_star_network

In these conditions, if propagation time was instant a miner’s revenue would be proportional to the share of the network hashrate it controls. Because it’s not, there is always a chance that a miner’s block goes stale because it enters a race with another miner’s competing block which it ends up losing.

In our model with uniform block propagation time s seconds, there is two situations in which a miner’s block may go stale:

  1. Another miner found a block s_b seconds (0 \lt s_b \lt s) before we did. All other miners receive the competing miner’s block first and start mining on top of it (or on a competing block of their own). Any of these miners then finds a second block on top.
  2. Another miner finds a block s_a seconds (0 \lt s_a \lt s) after we did. It immediately starts mining on top of it. Then the following block is also found by this same miner. Note how there may be more than one such miner competing against our block.

That a competing miner finds a second block does not technically guarantee to resolve the race, as a non-competing miner could also find a second block (before receiving the competing miner’s) and prolong the race. This probability decreases exponentially with the size of the fork. In this simplified analysis, we will assume that a competing miner finding a second block always lead to them winning the race.

Let’s call the first event Before and the second one After. For a given miner that just found a block, the probability that this block ends up stale is the probability that either of these two events happens. From this definition, it seems clear that the probability of Before is higher than that of After. Could it mean that miners care more about hearing others’ blocks faster than they care about publishing their own blocks faster? It also seems that the probability of After largely increases with mining centralization: one miner controlling 40% of the hashrate has a higher chance of finding two blocks in a row than 40 miners controlling 1% of the hashrate do. Finally, the probability of both events clearly decreases as a miner’s hashrate grows. But by how much?

We’ll analyze the probability of Before first. It’s worth pointing that one other miner finding a block s_b seconds before we do does not necessarily mean all other miners are mining on top of this competing miner’s block. It may be that some of them found a block before receiving it, and mine on top of their own. And it may be that the competing miner’s block is itself racing a previous block. But in all those cases, the rest of the network would be mining on top of a different block than that of the initial miner being studied. And this is all that matters to estimate the probability its block goes stale.

Given a miner controlling a share h of the network’s hashrate, the probability that the rest of the network had found a block at most s seconds before it did is 1 - \exp( -\frac{(1 - h) \cdot s}{600} ) [1]. Independently, the probability that the next block (whenever it arrives) is found by the rest of the network is 1 - h. We’ve established that if another miner had found a block s seconds or less before, then all the rest of the network mines on top of a block different from the block just found by this miner. Therefore the probability of event Before for this miner is simply:

P(Before) = (1 - \exp( -\frac{(1 - h) \cdot s}{600} ) ) \cdot (1 - h)

Now let’s look into the probability of After. The probability that any other miner (possibly more than one) finds a block within the s seconds of our miner finding one, and then the following block (whenever it arrives) is found by this same miner, will necessarily depend on the distribution of the rest of the network’s hashrate. Given such a distribution \mathbf{H} = (h_1, \ldots, h_n), the probability of After for miner i is:

P(After_i) = \sum_{\substack{1\le j\le |\mathbf{H}|\\ j\ne i}} (1 - \exp(-\frac{h_j \cdot t}{600})) \cdot h_j

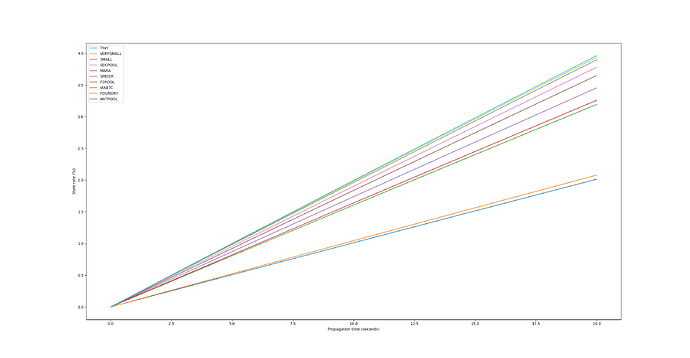
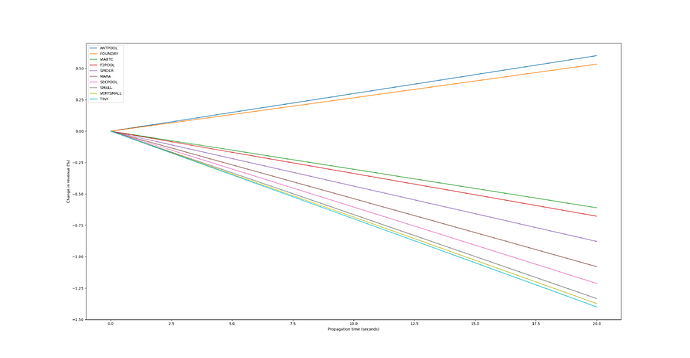
Given a hashrate distribution similar to that of the past 3 months, here is a couple graphs representing the impact of propagation time on mining centralization (source code here).

First, the stale rate of each pool in function of propagation time:

stale_rates
stale_rates2560×1331 249 KB

Consequently, the net benefit of each pool in function of propagation time (% change between share of network hashrate and share of blocks found):

net_benefits
net_benefits2560×1331 136 KB

I think it’s important to underline here that even a few basis points translate to material gains. Consider for instance the case of a mining operation controlling 5EH/s (about 0.5% of the network hashrate) choosing which mining pool to connect to. With an average block reward of 3.16BTC and an average USD/BTC rate of $110k, this operation can expect to generate about $91M in mining revenue over a year. If blocks took 10 seconds to propagate, choosing to mine on the largest pool rather than the smallest one would increase their revenue by $100k.

To confirm those numbers, i ran my mining simulation configured with a hashrate distribution similar[2] to that used to generate the graphs, for various uniform block propagation times:

0 seconds propagation time 
Running 32768 simulations in parallel using 16 threads.
100% progress..
After running 32768 simulations for 365d each, on average:
  - Miner 0 (30% of network hashrate) found 15779 blocks i.e. 30.0008% of blocks. Stale rate: 3.7317e-05%.
  - Miner 1 (29% of network hashrate) found 15253 blocks i.e. 28.9996% of blocks. Stale rate: 8.39912e-05%.
  - Miner 2 (12% of network hashrate) found 6311 blocks i.e. 12.0001% of blocks. Stale rate: 0.00018713%.
  - Miner 3 (11% of network hashrate) found 5785 blocks i.e. 10.9996% of blocks. Stale rate: 0.000215721%.
  - Miner 4 (8% of network hashrate) found 4207 blocks i.e. 7.99964% of blocks. Stale rate: 0.000245275%.
  - Miner 5 (5% of network hashrate) found 2629 blocks i.e. 4.99994% of blocks. Stale rate: 0.00029004%.
  - Miner 6 (3% of network hashrate) found 1577 blocks i.e. 3.00011% of blocks. Stale rate: 0.00029744%.
  - Miner 7 (1% of network hashrate) found 525 blocks i.e. 1.00003% of blocks. Stale rate: 0.000308817%.
  - Miner 8 (1% of network hashrate) found 526 blocks i.e. 1.00016% of blocks. Stale rate: 0.000338637%.
5 seconds propagation time 
Running 32768 simulations in parallel using 16 threads.
100% progress..
After running 32768 simulations for 365d each, on average:
  - Miner 0 (30% of network hashrate) found 15699 blocks i.e. 30.0456% of blocks. Stale rate: 0.506248%.
  - Miner 1 (29% of network hashrate) found 15172 blocks i.e. 29.037% of blocks. Stale rate: 0.523793%.
  - Miner 2 (12% of network hashrate) found 6260 blocks i.e. 11.9815% of blocks. Stale rate: 0.811484%.
  - Miner 3 (11% of network hashrate) found 5738 blocks i.e. 10.9818% of blocks. Stale rate: 0.825946%.
  - Miner 4 (8% of network hashrate) found 4171 blocks i.e. 7.98334% of blocks. Stale rate: 0.877786%.
  - Miner 5 (5% of network hashrate) found 2605 blocks i.e. 4.98683% of blocks. Stale rate: 0.928523%.
  - Miner 6 (3% of network hashrate) found 1562 blocks i.e. 2.99029% of blocks. Stale rate: 0.964853%.
  - Miner 7 (1% of network hashrate) found 520 blocks i.e. 0.996918% of blocks. Stale rate: 0.997677%.
  - Miner 8 (1% of network hashrate) found 520 blocks i.e. 0.996714% of blocks. Stale rate: 0.995936%.
10 seconds propagation time 
Running 32768 simulations in parallel using 16 threads.
100% progress..
After running 32768 simulations for 365d each, on average:
  - Miner 0 (30% of network hashrate) found 15620 blocks i.e. 30.0889% of blocks. Stale rate: 1.00885%.
  - Miner 1 (29% of network hashrate) found 15095 blocks i.e. 29.0779% of blocks. Stale rate: 1.04392%.
  - Miner 2 (12% of network hashrate) found 6210 blocks i.e. 11.963% of blocks. Stale rate: 1.61943%.
  - Miner 3 (11% of network hashrate) found 5691 blocks i.e. 10.9634% of blocks. Stale rate: 1.65332%.
  - Miner 4 (8% of network hashrate) found 4134 blocks i.e. 7.96494% of blocks. Stale rate: 1.75734%.
  - Miner 5 (5% of network hashrate) found 2581 blocks i.e. 4.97324% of blocks. Stale rate: 1.85906%.
  - Miner 6 (3% of network hashrate) found 1548 blocks i.e. 2.98236% of blocks. Stale rate: 1.93194%.
  - Miner 7 (1% of network hashrate) found 515 blocks i.e. 0.993453% of blocks. Stale rate: 2.00014%.
  - Miner 8 (1% of network hashrate) found 515 blocks i.e. 0.99282% of blocks. Stale rate: 2.00143%.
15 seconds propagation time 
Running 32768 simulations in parallel using 16 threads.
100% progress..
After running 32768 simulations for 365d each, on average:
  - Miner 0 (30% of network hashrate) found 15543 blocks i.e. 30.1333% of blocks. Stale rate: 1.50776%.
  - Miner 1 (29% of network hashrate) found 15018 blocks i.e. 29.1155% of blocks. Stale rate: 1.55891%.
  - Miner 2 (12% of network hashrate) found 6162 blocks i.e. 11.9478% of blocks. Stale rate: 2.43205%.
  - Miner 3 (11% of network hashrate) found 5645 blocks i.e. 10.9445% of blocks. Stale rate: 2.48371%.
  - Miner 4 (8% of network hashrate) found 4098 blocks i.e. 7.94632% of blocks. Stale rate: 2.64209%.
  - Miner 5 (5% of network hashrate) found 2558 blocks i.e. 4.96005% of blocks. Stale rate: 2.79304%.
  - Miner 6 (3% of network hashrate) found 1533 blocks i.e. 2.9729% of blocks. Stale rate: 2.90627%.
  - Miner 7 (1% of network hashrate) found 510 blocks i.e. 0.990086% of blocks. Stale rate: 3.00608%.
  - Miner 8 (1% of network hashrate) found 510 blocks i.e. 0.989569% of blocks. Stale rate: 3.01052%.
20 seconds propagation time 
Running 32768 simulations in parallel using 16 threads.
100% progress..
After running 32768 simulations for 365d each, on average:
  - Miner 0 (30% of network hashrate) found 15469 blocks i.e. 30.1808% of blocks. Stale rate: 2.002%.
  - Miner 1 (29% of network hashrate) found 14943 blocks i.e. 29.154% of blocks. Stale rate: 2.07079%.
  - Miner 2 (12% of network hashrate) found 6113 blocks i.e. 11.9273% of blocks. Stale rate: 3.24164%.
  - Miner 3 (11% of network hashrate) found 5600 blocks i.e. 10.9257% of blocks. Stale rate: 3.31431%.
  - Miner 4 (8% of network hashrate) found 4064 blocks i.e. 7.92956% of blocks. Stale rate: 3.52448%.
  - Miner 5 (5% of network hashrate) found 2535 blocks i.e. 4.94618% of blocks. Stale rate: 3.7338%.
  - Miner 6 (3% of network hashrate) found 1519 blocks i.e. 2.9636% of blocks. Stale rate: 3.87825%.
  - Miner 7 (1% of network hashrate) found 505 blocks i.e. 0.986592% of blocks. Stale rate: 4.02113%.
  - Miner 8 (1% of network hashrate) found 505 blocks i.e. 0.98618% of blocks. Stale rate: 4.02959%.

When considering a change in the P2P network, it is hard to evaluate the impact it would have on the stale rate. This problem can be decomposed in two parts: how the change would likely affect block propagation times, and how the estimated effect on block propagation times would in turn affect the stale rate. I hope this simplified model can give us some insights on the latter.

  1. CDF of the exponential distribution with mean 600. ↩︎

  2. My C++ simulation at the moment requires integer values for shares of network hashrate controlled, so the hashrate controlled by the made-up SMALL, VERYSMALL and TINY pools was changed. ↩︎

3 Likes
2

Average revenue isn’t the right model, the reality is much worse– much of that $91m will go to power costs, right? So the miner’s net profits is increased by a much larger factor.

The actual impact on the network is hard to judge esp post compact blocks stales are much less visible. Ideally the protocol would get some new “STALEHEADER” message for relaying headers that connect near the best chain tip*– without implying an ability to serve the block–, for stats purposes.

*(e.g. relay along any stale header that connects to a block within 10 of the tip, or to one of the last 10 accepted stale headers, so it also lets you view large invalid forks– so long a POW validity and difficulty logic are enforced it shouldn’t have any DOS risk, assuming it’s only activated once the chain has met minimum chain work)

3

Related benchmarking Stratum V2 - Next Generation Bitcoin Mining Protocol

4

Right, but profit is a function of revenue. Since i did not have a model for this function i just let the “raw” revenues.

But yes maybe it’s worth expliciting: mining is a thin margins business. A 0.05% drop in revenue may well be a 5% drop in profits.

I discussed this with other Bitcoin developers a week ago and this came up. I think this makes sense and should be pretty straightforward.