Untraceable Taprootized Atomic Swaps

Protocol Design
1

Taprootized Atomic Swaps

Taprootized Atomic Swaps (TAS) is an extension for Atomic Swaps that presumes the untraceability of transactions related to a particular swap. Based on Schnorr signatures, Taproot technology, and zero-knowledge proofs, the taprootized atomic swaps hide swap transactions under regular payments.

Intro

Atomic swap is an incredible approach to cross-chain exchanges without mediators. However, one of the disadvantages of its implementation in the classical form is the “digital trail” — any party can make a matching between transactions in the blockchains in which the exchange took place and find out both the participants in the exchange and the proportion in which assets were exchanged.

On the other hand, atomic swaps is a technology that initially assumed the involvement of only two parties and a “mathematical contract” between them directly. That is, an ideal exchange presupposes two conditions:

  1. Only counterparties participate in the exchange (works by default)
  2. Only counterparties know about the fact of the exchange (it would be nice to ensure)

This paper will provide a concept of taprootized atomic swaps that allow hiding the swap’s very fact. To an external auditor, transactions to initiate and execute atomic swaps will be indistinguishable from regular Bitcoin payments. In the other accounting system involved in the transfer, more information is disclosed (the fact of exchange can be traced). Still, it is impossible to link this to the corresponding Bitcoin transactions (without additional context from the involved parties).

Protocol

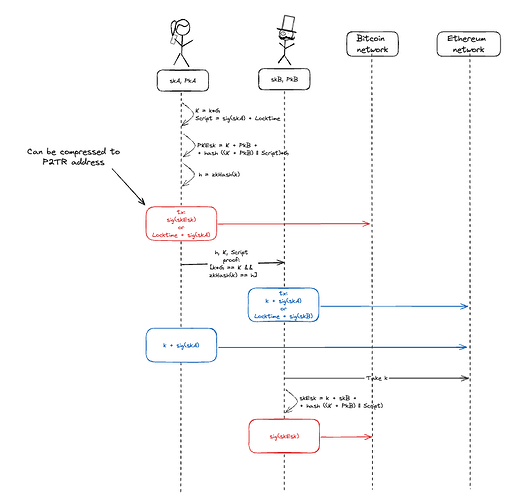
Screenshot 2024-01-22 at 20.29.06
Screenshot 2024-01-22 at 20.29.06763×720 32.3 KB

The protocol includes the following steps:

  1. Alice (skA, PKA) and Bob (skB, PKB) have their keypairs and know each other’s public keys.
  2. Alice generates a random k and calculates the public value K = k * G
  3. Alice forms the alternative spending path Script = sig(skA) + Locktime in the form of Bitcoin Script
  4. Alice calculates an escrow public key as PKEsc = K + PKB + hash((K + PKB) || Script) * G (here, escrow is just a public key, formed using Taproot technology)
    1. The signature sig(skEsc), verified by the PKEsc, can be generated only with the knowledge of k, skB, and Script
  5. Alice calculates h as a hash value of k (zk-friendly hash function is recommended to use)
  6. Alice forms the funding transactions with the following conditions of how it can be spent:
    1. Signature of skEsc: Bob, with knowledge of k and skB can spend the output
    2. Signature of skA + Locktime: Alice, with knowledge of skA can spend the output, but only after some point in time t1 (the Script itself)
  7. Alice sends the transaction to the Bitcoin network
  8. Alice generates the zero-knowledge proof that includes (for the same k):
    1. The proof of knowledge of k that satisfies kG == K*
    2. The proof of knowledge of k that satisfies zkHash(k) == h
  9. Alice provides the set of data to Bob:
    1. h
    2. K
    3. Script
    4. proof
  10. Bob calculates PKEsc as K + PKB + hash((K + PKB) || Script) * G and finds the transaction locked BTC (verifies if it exists). Then Bob performs the following verifications:
    1. Verifies that Alice knows k that satisfies kG == K* and zkHash(k) == h, it means that Bob can access the output PKEsc if he receives k
    2. Verifies that the Script is correct and includes only the required alternative path.
  11. If verifications are passed, Bob forms the transaction that locks his funds on the following conditions:
    1. Publishing of k and the signature of skA: only Alice can spend it if she reveals k (hash preimage)
    2. Signature of skB + Locktime: Bob, with knowledge of skB, can spend the output, but only after some point in time t2
  12. Bob sends the transaction to the Ethereum network (or any other that supports zkHash())
  13. Alice sees the locking conditions defined by Bob and publishes the k and the signature generated by her skA. As a result — Alice spent funds locked by Bob.
    1. If Alice doesn’t publish the relevant k, Bob can return funds after t2 is reached
  14. If Alice publishes a transaction with k, Bob can recognize it and extract the k value
  15. Bob calculates the needed skEsc as skEsc = k + skB + hash((K + PKB) || Script)
  16. Bob sends the transaction with the signature generated by the skEsc and spends funds locked by Alice

Implementation notes

  1. As an approach for escrow public key forming, the MuSig aggregation mechanism is preferable [1].
  2. All conditions described in step 5 (Protocol section) can be put into a P2TR address. The formed address will not differ from the regular Bitcoin address (single or multisig) formed using the P2TR method [2].
  3. As a zk-friendly hash function, we can use Poseidon [3].
  4. For zk operations with EC points, we can use the 0xPARC library [4].

Links

[1] MuSig | Bitcoin Optech

[2] bips/bip-0341.mediawiki at deae64bfd31f6938253c05392aa355bf6d7e7605 · bitcoin/bips · GitHub

[3] circomlib/circuits/poseidon.circom at cff5ab6288b55ef23602221694a6a38a0239dcc0 · iden3/circomlib · GitHub

[4] circom-ecdsa/circuits/secp256k1.circom at d87eb7068cb35c951187093abe966275c1839ead · 0xPARC/circom-ecdsa · GitHub

P.S. The original doc is here Taprootized Atomic Swaps - Google Docs

1 Like
2

Hi @olkurbatov,

How does this compare to a PTLC?

1 Like
3

I’m now thinking about how to use signature adapters (and PTLC) on the second side to make the protocol even more private:

  1. Basic signature adapters do not protect from the situation where one party can take money from both outputs (with the knowledge of t). Hence, you need to add a multisignature to the adapters. In the TAS case, the escrow key is formed in such a way that only Bob can take it after Alice publishes the secret.
  2. This should work seamlessly with both Schnorr signatures and classic ECDSA. Atomic swaps like here require musig
  3. Just today, we made such a swap between Bitcoin and Ethereum:

Parameters used for the swap k: b550385a62c0eba5a837ee11962e380818a50611caa1113e33a411528ebb193d; K: 03d39da41952d4ae038a49b693b313ec956ad80d9fc940dc5afedf86351e9fa930

Transactions:

  1. Alice locks BTC: 850e9258bf8b3bb280d32a647198d8024aece543dc283f7bfa526f4c0ceb1ab8
  2. Bob locks ETH: 723919c0e8ec57d38792ec29b2cb82ee885b9fbbc886b34ff40fb5d3f7cc9b43
  3. Alice withdraws ETH from the contract: 47546191a7c99ec4a7ddc243d6ea75d345ab3aff0762e09dd2f537731bd484f3
  4. Bob spends BTC: 859dbfaa901d7106aecc8cb29966ede0c9d7a17c2cae31f4d420c1d770e9706d

The demo code: GitHub - distributed-lab/taprootized-atomic-swaps: Taprootized Atomic Swaps (TAS) is an extension for Atomic Swaps that presumes the untraceability of transactions related to a particular swap.

1 Like