Determining BlockTemplate Fee Increase Using Fee Rate Diagram

ismaelsadeeq · October 13, 2025, 2:20pm

Motivation and Background

Currently, when miners want to determine whether a block template with more fees is available, they repeatedly poll the getblocktemplate RPC until a better template is returned (relative to the one they are working on). This approach can lead to redundant block template builds in some cases.

The experimental mining interface introduced in Bitcoin Core v30, waitnext(), improves this by allowing clients to wait and receive a new block template after a noticeable fee increase or when the blockchain tip changes.

However, internally, waitnext() also regenerates block templates every second. Building a block template locks Bitcoin Core mutexes, (mempool (cs) and cs_main) throughout the build. These locks prevent concurrent access during template generation for thread safety purpose, which can delay transaction processing and relay to peers.

A better approach is to track the potential fee increase resulting from each mempool update that affects the current block template. The node can then decide whether rebuilding the template is worthwhile based on the accumulated fee increase.

Implementing this in current Bitcoin Core is challenging because, for each mempool update, the effective chunk fee rate of affected transactions is not explicitly known [0].

However, with the introduction of the Cluster Mempool [1], this limitation no longer applies.

This post explores a simple method that leverages Cluster Mempool feature to determine whether there has been a potential fee rate improvement in a block template without requiring a full rebuild.

Prerequisites

Definitions

Fee Rate: The fee of a transaction divided by its size.
Chunk: A grouped list of related transactions that should be mined together.
Chunk Fee Rate: The total fees of all transactions in a chunk divided by their total size.
Fee Rate Diagram: A monotonically decreasing list of chunks used to plot a graph where the y-axis represents the fee and the x-axis represents transaction size.

Block Template Fee Increase

The objective is to determine the potential fee increase of a block template as the mempool evolves, without rebuilding the block template using the node’s block assembler.

Given a previously built block template, compute/save:

\begin{aligned} F_{\text{threshold}} &= \text{(the fee increase that warrants a new block template build)} \\ F &= \sum_{i=1}^{n} f_i \text{( sum of fees of all chunks in the current block template)} \\ S &= \sum_{i=1}^{n} s_i \text{( sum of size of all chunks in the current block template)} \\ F_{\text{modified}} &= F \text{(modified total fee after mempool updates)} \\ S_{\text{modified}} &= S \text{(modified total size after mempool updates)} \\ W &= \text{maximum allowed block weight} \\ L &= \text{the lowest-fee-rate (worst) chunk currently in the block template} \\ A &= \lbrace\rbrace \text{(list of newly added chunks with } r_i > r_L \text{, sorted descending by fee rate)} \\ R &= \lbrace\rbrace \text{(list of removed chunks with } r_i \ge r_L \text{, sorted ascending by fee rate)} \\ r_i &= \frac{f_i}{s_i} \text{(fee rate of chunk } i) \end{aligned}

Mempool Update Scenarios

When a new transaction enters the mempool, two primary cases occur:

Addition without in-mempool conflicts The transaction connects to zero or more existing clusters. A new linearization is computed for the affected clusters, producing both an old and new fee rate diagram.
Addition with in-mempool conflicts The transaction conflicts with one or more existing transactions in the mempool. The connected clusters are re-linearized, generating both old and new fee rate diagrams.

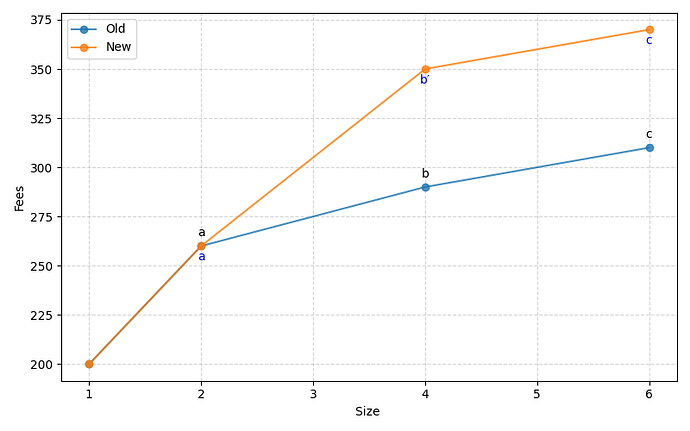
Naive example of mempool addition of b′ that improves the fee rate of b.

In both cases, the addition is accepted iff the new fee rate diagram is strictly better.

There is also a rare case where update has only the old diagram, for example, when the mempool is full and the lowest-fee chunk is evicted. This is uncommon, as miners typically run nodes with large mempools, but it should still be handled.

After an Update

If there is an old diagram:

Initialize an empty temporary list \text{New}_R = \{\}.

For each chunk c in the old fee rate diagram, if r_c \ge r_L, add c to \text{New}_R.

Maintain \text{New}_R in ascending order by fee rate.

Iterate through \text{New}_R:

For each chunk c \in \text{New}_R (from lowest fee rate):

\begin{cases} \text{if } c = L: & \text{Remove } L \text{ from block template} \\ & \text{Update } L \text{ to the new worst chunk in the remaining block template} \\ & \text{Remove } c \text{ from } \text{New}_R \\ & F_{\text{modified}} \leftarrow F_{\text{modified}} - f_c \\ & S_{\text{modified}} \leftarrow S_{\text{modified}} - s_c \\ \text{else if } r_c > r_L: & \text{Exit loop — all remaining chunks have } r_c > r_L \end{cases}

After the loop, add all remaining chunks in \text{New}_R to the persistent set R (chunks with r_c > r_L that were removed but not equal to the old L).

If there is a new diagram:

For each chunk c in the new fee rate diagram, if r_c > r_L, add c to A (maintained in descending fee rate order).

Evaluating Potential Fee Increase

Phase 1: Remove evicted chunks from block template

Loop through the block template chunks. For each chunk c:

If any chunk in R matches c, remove it from the block template. Subtract its fees from F_{\text{modified}} and its size from S_{\text{modified}}.

Clear R afterward.

Phase 2: Perform naive merge

Initialize:

F_{\text{naive}} = F_{\text{modified}}, \quad S_{\text{naive}} = S_{\text{modified}}

Iterate through chunks in A (in descending fee rate order):

\text{for each chunk } a_i \in A:

If S_{\text{naive}} + s_{a_i} \le W, then:

\begin{cases} F_{\text{naive}} \leftarrow F_{\text{naive}} + f_{a_i} \\ S_{\text{naive}} \leftarrow S_{\text{naive}} + s_{a_i} \end{cases}

Compute:

\Delta F = F_{\text{naive}} - F

If \Delta F \ge F_{\text{threshold}}: rebuild the block template.
If all chunks in A are added and \Delta F < F_{\text{threshold}}: stop (insufficient improvement).

Phase 3: Iterative merge (if naive merge is inconclusive)

If the naive merge shows potential but is inconclusive, perform an iterative merge of the block template chunks and chunks in A:

Initialize an empty block template and fill it by selecting the best chunks from both the existing template and A.
Stop when:
- Block weight W is reached,
- No chunk from the template or A will fit, or
- The iteration limit is reached.

Compute:

\Delta F_{\text{new}} = F_{\text{new}} - F

If \Delta F_{\text{new}} \ge F_{\text{threshold}}: build and return the new block template.

Phase 4: Update state

After building a new block template:

Clear A
Set the new template as the current one
Update L to the worst chunk in the new template
Update F_{\text{modified}} = F_{\text{new}}, S_{\text{modified}} = S_{\text{new}}

Implementation Note

This computation can be handled asynchronously by a Block Template Manager (as proposed in Bitcoin Core Issue #33389). It should operate independently of cs_main and mempool locks by using a validation interface notification executed in a scheduler thread after each mempool update. This notification provides both old and new fee rate diagrams, which is also useful for the block policy estimator [2]. The Block Template Manager maintains its own internal locks to ensure thread safety without blocking mempool or transaction relay operations.

Limitation

This approach does not account for bin-packing effects at the block template tail [3].

References

[0] Proposal for a new mempool design

[1] Cluster Mempool

[2] Package-Aware Fee Estimator Post Cluster Mempool

[3] Bin Packing Problem

Original post Determining Block Template Fee Increase Using Fee Rate Diagram deleted mistakenly sorry for the noise

sipa · October 13, 2025, 2:49pm

I think the same estimate is possible without actually maintaining the template set R, even incrementally.

Inside TxGraph (the internal component abstracting away the cluster linearization complexity from the mempool), we currently maintain an index of all chunks, sorted by descending feerate. This index is totally ordered, and is used for block building and eviction, but can be used for more than that.

The idea would be to maintain an implicit block template, consisting of all chunks in TxGraph from the beginning of the index, up to but excluding a non-fitting chunk c_\mathrm{nf}, so F = \sum_{c=0}^{c < c_\mathrm{nf}} \mathrm{fee}(c), and S = \sum_{c=0}^{c < c_\mathrm{nf}} \mathrm{size}(c). The non-fitting chunk c_\mathrm{nf} is such that S \leq 3992000, but S + \mathrm{size}(c_\mathrm{nf}) > 39920000. TxGraph stores F, S, and a pointer to c_\mathrm{nf}.

After any operation that modifies TxGraph, these variables can be updated. If a chunk c is removed for which c < c_\mathrm{nf}, subtract it from (F, S). If a chunk c is added for which c < c_\mathrm{nf}, add it to (F, S). If the pointed-to chunk itself is removed, move the pointer up, c_\mathrm{nf} := c_\mathrm{nf} + 1. If at the end S + \mathrm{size}(c_\mathrm{nf}) \leq 3992000, add it to (F, S) and move the pointer up. If at the end S > 3992000, subtract from (F, S) and move the pointer down.

These operations are all \mathcal{O}(n) in the number of modified chunks, so don’t change any internal complexity, and they only need \mathcal{O}(1) memory (F, S, and one pointer).

And with these variables, we can associate two block fee estimates:

A conservative lower bound: F.
A conservative upper bound: F + \frac{\mathrm{fee}(c_\mathrm{nf})}{\mathrm{size}(c_\mathrm{nf})} \cdot (3992000 - S).

A combination of the two could be used as approximation.

My idea would be to allow the block template waiting code to install a callback function into TxGraph, which would get called any time the lower/upper bound change. The callback function could then decide whether the increase since the last computed block template is significant enough to trigger a full block templating building.

ismaelsadeeq · October 13, 2025, 3:18pm

Nice, this is better it removes the need to maintain a list of removed chunks! The reason I wanted the process to be independent of the mempool and txgraph is to avoid adding additional computational requirements after each commit to the txgraph main, as well as when the lower or upper bounds change.