Benchmark results
All data is tested in 6 different linearization settings:
- CSS: the candidate-set search algorithm this thread was initially about, both from scratch and when given an optimal linearization as input already.
- SFL: the spanning-forest linearization algorithm, also from scratch and when given an optimal linearization as input already.
- GGT: the parametric min-cut breakpoints algorithm from the 1989 GGT paper, both its full bidirectional version, and a variant that only runs in the forward direction.
Simulated 2023 mempools
This uses clusters that were created by replaying a dump of 2023 P2P network activity into a cluster-mempool-patched version of Bitcoin Core (by @sdaftuar), and storing all clusters that appear in a file. This included 199076 clusters of size between 26 and 64 transactions, and over 24 million clusters between 2 and 25 transactions. Note that this is not necessarily representative for what a post-cluster-mempool world will look like, as it enforces a cluster size limit of 64, which may well influence network behavior after adoption.
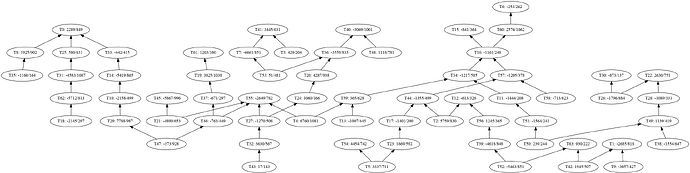
Here are two example 64-transaction clusters:
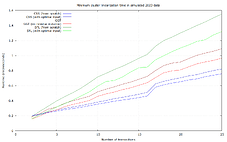
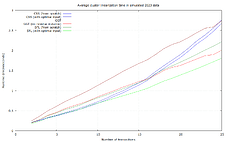
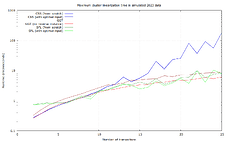
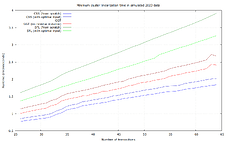
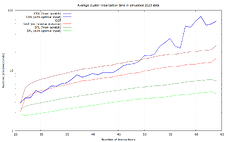
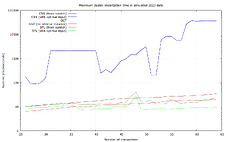
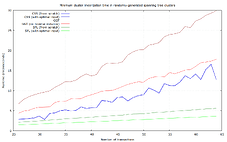
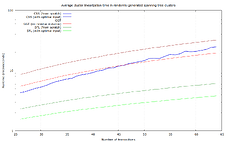
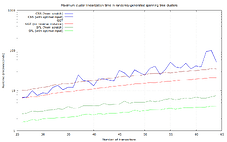
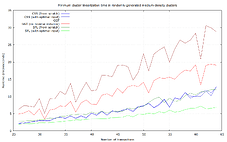
Numbers for 2-25 transaction clusters, based on benchmarks of 7.5% of the recorded clusters:
Numbers for 26-64 transaction clusters, benchmarking all of the clusters:
For sufficiently large clusters, and in average and maximum runtime, SFL is the clear winner in this data set. CSS has better lower bounds, but is terrible in the worst case (31.5 ms).
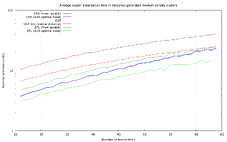
Randomly-generated tree-shaped clusters
In this dataset, for each size between 26 and 64 transactions, 100 random tree-shaped clusters (i.e., a connected graph with exactly n-1 dependencies) were generated, like this 64-transaction one:
Again, SFL seems the clear winner.
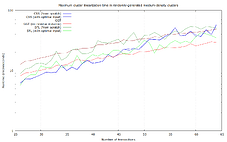
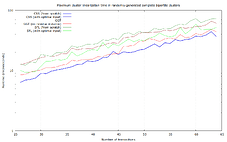
Randomly-generated medium-density clusters
In this dataset, for each size between 26 and 64 transactions, 100 random spanning-tree clusters (with roughly 3 dependencies per transaction) were generated, like this 64-transaction one. I promise this is not the plot of Primer (2004):
Notably, SFL performs worst in the worst case here, with up to 83.1 μs runtime, though even the fastest algorithm (unidirectional GGT) even takes up to 30.2 μs. This is probably due to it inherently scaling with the number of dependencies.
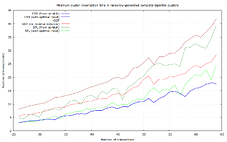
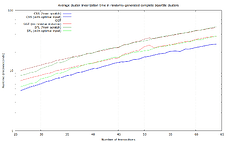
Randomly-generated complete bipartite clusters
In this dataset, for each size between 26 and 64 transactions, 100 random complete-connected bipartite clusters (with roughly n/4 dependencies per transaction) were generated, like this 64-transaction one:
With even more dependencies per transaction here, SFL’s weakness is even more visible (up to 114.8 μs), though it affects GGT too. Note that due to the large number of dependencies, these clusters are expensive too: if all the inputs and outputs are key-path P2TR, then the 64-transaction case needs ~103 kvB in transaction input & output data.
Methodology
All of these numbers are constructed by:
- Gather a list of N clusters (by replaying mempool data, or randomly generating them).
- For each of the N cluster, do the following 5 times:
- Generate 100 RNG seeds for the linearization algorithm.
- For each RNG seed:
- Benchmark optimal linearization 13 times with the same RNG seed, on an AMD Ryzen 9 5950X system.
- Remember the median of those 13 runs, to weed out variance due to task swapping and other effects).
- Remember the average of those 100 medians, as we care mostly about how long the duration of linearization many clusters at once is, not an individual one. This removes some of the variance caused by individual RNG seeds.
- Output the minimum, average, and maximum of those 5N average-of-medians.
All the data and graphs can be found on Cluster linearization databench plotting code · GitHub.